题目内容
⊙O中,弦AB=| 3 |
 |
| AB |
分析:如图,由C为劣弧
的中点,根据垂径定理的推论得到OC⊥AB,AD=BD,而AB=
,OA=1,根据勾股定理得到DO=
,即D为OC的中点,OC和AB相互垂直平分,根据菱形的判定方法即可得到四边形OACB的形状.
 |
| AB |
| 3 |
| 1 |
| 2 |
解答: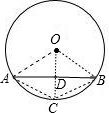 解:如图,连OA,OB,AC,BC,OC,OC与AB交于点D,
解:如图,连OA,OB,AC,BC,OC,OC与AB交于点D,
四边形OACB为菱形.理由如下:
∵C为劣弧
的中点,
∴OC⊥AB,AD=BD,
又∵AB=
,OA=1,
∴AD=
,DO=
,而OC=1,
∴D为OC的中点,
∴四边形OACB为菱形.
 解:如图,连OA,OB,AC,BC,OC,OC与AB交于点D,
解:如图,连OA,OB,AC,BC,OC,OC与AB交于点D,四边形OACB为菱形.理由如下:
∵C为劣弧
 |
| AB |
∴OC⊥AB,AD=BD,
又∵AB=
| 3 |
∴AD=
| ||
| 2 |
| 1 |
| 2 |
∴D为OC的中点,
∴四边形OACB为菱形.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了垂径定理和勾股定理以及菱形的判定方法.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.
如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB. 7、如图,在⊙O中,弦AB,CD相交于点E.已知∠ECB=60°,∠AED=65°,那么∠ADE的度数是( )
7、如图,在⊙O中,弦AB,CD相交于点E.已知∠ECB=60°,∠AED=65°,那么∠ADE的度数是( )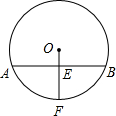 如图,⊙O中,弦AB=12cm,点E是AB中点,连接OE并延长交⊙O于点F,若EF=4cm,求⊙O的半径.
如图,⊙O中,弦AB=12cm,点E是AB中点,连接OE并延长交⊙O于点F,若EF=4cm,求⊙O的半径.