题目内容
 如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.
如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.(1)求证:△PAC与△PDB是否相似
(2)当
| AC |
| DB |
| S△PAC |
| S△PDB |
分析:(1)利用圆周角定理的推论,同弧所对的圆周角相等,可以得到三角形的相似.
(2)利用面积比等于相似比的平方求解.
(2)利用面积比等于相似比的平方求解.
解答:(1)证明:∵∠A=∠D,∠C=∠B,
∴△PAC∽△PDB;
(2)解:∵△PAC∽△PDB,
=(
)2=4,
∴
=2.
∴△PAC∽△PDB;
(2)解:∵△PAC∽△PDB,
| S△PAC |
| S△PDB |
| AC |
| DB |
∴
| AC |
| DB |
点评:此题运用了圆周角定理的推论,还用到了相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目
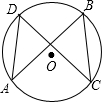 已知:如图,在⊙O中,弦AD=BC.求证:AB=CD.
已知:如图,在⊙O中,弦AD=BC.求证:AB=CD. 4、如图,在⊙O中,弦BC∥半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( )
4、如图,在⊙O中,弦BC∥半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( ) 标系.
标系. 如图,在⊙O中,弦AB=BC=CD,且∠ABC=140°,则∠AED=( )
如图,在⊙O中,弦AB=BC=CD,且∠ABC=140°,则∠AED=( ) 如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.
如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.