题目内容
5.要使方程组$\left\{\begin{array}{l}{{x}^{2}+2ay=5}\\{y-x=6a}\end{array}\right.$有正整数解,则a的值是$\frac{1}{2}$,$\frac{1}{6}$.分析 审题可知这是一道含有字母系数的二次方程组,首先代入消元得到含有字母a的一元二次方程:x2+2ax+12a2-5=0,用公式法求出方程的根-a±$\sqrt{5-11{a}^{2}}$:利用判别式分析得出a<$\frac{8}{11}$,再根据“解为正整数,y-x=6a”得出6a为整数,a的绝对值只能取值为:$\frac{2}{3}$,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$,最后代入根的公式,根据解为正整数进行检验.
解答 解:
方程组消元得:x2+2ax+12a2-5=0
用公式法求得方程的根为:x=-a±$\sqrt{5-11{a}^{2}}$,由△=-44a2+20≥0,得出|a|≤$\sqrt{\frac{5}{11}}$,
由x和y都是正整数知y-x=6a为整数,所以|a|的可能值为:$\frac{2}{3}$,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$
把a的值代入求根公式计算:当a=$\frac{1}{2}$时,x=-a±$\sqrt{5-11{a}^{2}}$,x=1(满足题意)或x=-2(舍去)
当a=$\frac{1}{6}$时,x=-a±$\sqrt{5-11{a}^{2}}$,x=2(满足题意)或x=$-\frac{7}{3}$(舍去)
依次验证得出:只有$\frac{1}{2}$和$\frac{1}{6}$满足题意.
故答案为:$\frac{1}{2}$,$\frac{1}{6}$.
点评 此题主要考查了方程组的消元法,以及对于一元二次方程的根的探索研究,在解决此题时,认真分析,分别讨论是关键,做题一定不要漏解.

练习册系列答案
相关题目
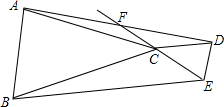 在△ABC和△DCE中,∠ACB=∠DCE=∠BEC,AC=BC,DC=EC,试说明AF=DF.
在△ABC和△DCE中,∠ACB=∠DCE=∠BEC,AC=BC,DC=EC,试说明AF=DF.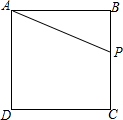 如图所示,正方形ABCD的边长为5,P为BC上一动点(不与B、C两点重合),若CP=x,△ABP的面积为y,求出y与x之间的函数关系式,并写出自变量x的取值范围.
如图所示,正方形ABCD的边长为5,P为BC上一动点(不与B、C两点重合),若CP=x,△ABP的面积为y,求出y与x之间的函数关系式,并写出自变量x的取值范围.