题目内容
20.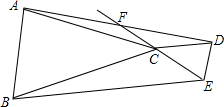 在△ABC和△DCE中,∠ACB=∠DCE=∠BEC,AC=BC,DC=EC,试说明AF=DF.
在△ABC和△DCE中,∠ACB=∠DCE=∠BEC,AC=BC,DC=EC,试说明AF=DF.
分析 作AM∥CD交EF的延长线于M,在BE上截取BN,使得BN=CM,易得△ACM≌△CBN,利用全等三角形的性质可得AM=CN,∠CMA=∠BNC,由平行线的性质可得∠CMA=∠FCD,等量代换可得∠CNE=∠DCE=∠CEN,证得CD=AM,由平行四边形的判定定理得四边形AMDC是平行四边形,利用平行四边形的性质得出结论.
解答 解:作AM∥CD交EF的延长线于M,在BE上截取BN,使得BN=CM,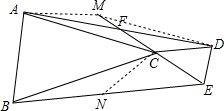
∵∠ACB=∠DCE=∠BEC,
∴CD∥BE,
∴∠CBE+∠DCB=180°,
∴∠CBE+∠BCE+∠ECD=180°,
∵∠ACB+∠BCE+∠ACM=180°,
∴∠CBE=∠ACM,
在△ACM与△CBN中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACM=∠CBN}\\{CM=BN}\end{array}\right.$,
∴△ACM≌△CBN(SAS),
∴AM=CN,∠CMA=∠BNC,
∵AM∥CD,
∴∠CMA=∠FCD,
∵∠FCD+∠DCE=180°,∠BNC+∠ENC=180°,
∴∠CNE=∠DCE=∠CEN,
∴CN=CE=CD,
∴CD=AM,
∴四边形AMDC是平行四边形,
∴AF=FD.
点评 本题主要考查了全等三角形与平行四边形的判定及性质定理,作出恰当的辅助线构建全等三角形,综合利用各定理是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图示,函数y=x+b和y=ax+3的图象交点为P,则不等式ax+3-x-b>0的解集为x<1.
如图示,函数y=x+b和y=ax+3的图象交点为P,则不等式ax+3-x-b>0的解集为x<1. 已知一个正方体所有相对的面上两数之和相等.如图是它的展开图,请填出图中空白正方形中的数.
已知一个正方体所有相对的面上两数之和相等.如图是它的展开图,请填出图中空白正方形中的数. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为2.
如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为2.