题目内容
（1）如图①，在△ABC中，AB=CD，∠BAD=∠BDA，AE是BD边的中线．探究AC与AE的数量关系并证明．
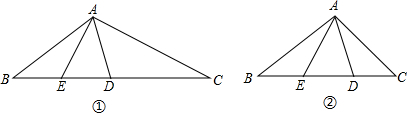
（2）如图②，在△ABC中，AB=k•AD，∠BAD=∠BDA，AE是BD边的中线，且∠EAD=∠C．探究AC与AE的数量关系并证明．
（2）如图②，在△ABC中，AB=k•AD，∠BAD=∠BDA，AE是BD边的中线，且∠EAD=∠C．探究AC与AE的数量关系并证明．
考点：相似三角形的判定与性质,全等三角形的判定与性质
专题：
分析：（1）作AC边上的中线，利用三角形的中位线的性质，得出相应的边和角的关系，进一步证出△ADF≌△ADE，得出结论即可；
（2）易得△ACE∽△DAE，则可得
=
=
=
=
=
．
（2）易得△ACE∽△DAE，则可得
| AC |
| AE |
| 2AD |
| 2ED |
| 2AD |
| BD |
| 2AD |
| AB |
| 2AD |
| kAD |
| 2 |
| k |
解答：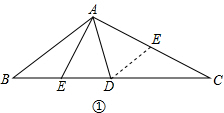
（1）答：AC=2AE．
证明：在△ACD中，作AC边上的中线DF，
∵∠BAD=∠BDA，
∴△ABD为等腰三角形，
∴AB=BD=CD，于是D为BC边上的中点，
∴DF为△ABC的中位线，DF=
AB=
BD，∠FDC=∠B，
∵AE是△ABD的中线，
∴ED=DF，
由于∠BDA+∠ADF+∠FDC=180°，
在△ABD中，∠B+∠BAD+∠BDA=180°，
∠FDC=∠B，∠BAD=∠BDA，
∴∠ADF=∠BDA，
在△ADF和△ADE中，
，
∴△ADF≌△ADE，
∴AE=AF，
∴AC=2AE．
（2）解：∵∠EAD=∠C，∠AED=∠CEA，
∴△ACE∽△DAE，
∴
=
，
即
=
，
∴
=
=
=
=
=
．
（1）答：AC=2AE．证明：在△ACD中，作AC边上的中线DF，
∵∠BAD=∠BDA，
∴△ABD为等腰三角形，
∴AB=BD=CD，于是D为BC边上的中点，
∴DF为△ABC的中位线，DF=
| 1 |
| 2 |
| 1 |
| 2 |
∵AE是△ABD的中线，
∴ED=DF，
由于∠BDA+∠ADF+∠FDC=180°，
在△ABD中，∠B+∠BAD+∠BDA=180°，
∠FDC=∠B，∠BAD=∠BDA，
∴∠ADF=∠BDA，
在△ADF和△ADE中，
|
∴△ADF≌△ADE，
∴AE=AF，
∴AC=2AE．
（2）解：∵∠EAD=∠C，∠AED=∠CEA，
∴△ACE∽△DAE，
∴
| AC |
| AD |
| AE |
| ED |
即
| AC |
| AE |
| AD |
| ED |
∴
| AC |
| AE |
| 2AD |
| 2ED |
| 2AD |
| BD |
| 2AD |
| AB |
| 2AD |
| kAD |
| 2 |
| k |
点评：此题考查了相似三角形的判定与性质、全等三角形的判定与性质以及等腰三角形的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，若BE⊥CD，BE=DE，BC=DA，则∠CFD（ ）| A、大于90° | B、等于90° |
| C、小于90° | D、不能确定 |
如图是由若干个相同小正方体组合而成的几何体，从左面、上面观察这个几何体，请分别画出你所看到的几何体的形状图．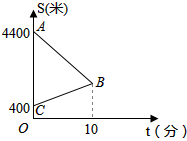
某天，小明来到体育馆看球赛，在距离体育场400米处的超市买水时发现门票还在家里，此时离比赛开始还有20分钟，于是立即步行回家取票．同时，他父亲从家里出发骑自行车以他4倍的速度给他送票，两人在途中相遇后，小明立即以原步行速度的1.2倍赶回体育馆．如图中线段AB、BC分别表示父子送票、儿子取票过程中，离体育馆的路程S（米）与所用时间t（分钟）之间的函数关系，结合图象解答下列问题：