题目内容
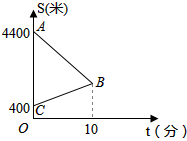 某天,小明来到体育馆看球赛,在距离体育场400米处的超市买水时发现门票还在家里,此时离比赛开始还有20分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他4倍的速度给他送票,两人在途中相遇后,小明立即以原步行速度的1.2倍赶回体育馆.如图中线段AB、BC分别表示父子送票、儿子取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题:
某天,小明来到体育馆看球赛,在距离体育场400米处的超市买水时发现门票还在家里,此时离比赛开始还有20分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他4倍的速度给他送票,两人在途中相遇后,小明立即以原步行速度的1.2倍赶回体育馆.如图中线段AB、BC分别表示父子送票、儿子取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题:(1)求AB所在直线的解析式.
(2)小明能否在比赛开始之前赶回体育馆?若能,请说明理由;若不能,小明取到票后,至少一原速度的多少倍才能在比赛前到达?
考点:一次函数的应用
专题:
分析:(1)设小明速度是x米/分,则小明父亲的速度是4x米/分.根据等量关系“小明速度×10+父亲速度×10=4400-400”列出方程求得x的值;则易求点B的纵坐标;然后把点A、B的坐标代入直线AB所在直线的解析式y=kx+b(k≠0),即利用待定系数法求该一次函数的解析式;
(2)计算一下小明返回体育场的时间,然后与20分钟作一比较即可判断明能否在比赛开始之前赶回体育馆.
(2)计算一下小明返回体育场的时间,然后与20分钟作一比较即可判断明能否在比赛开始之前赶回体育馆.
解答:解:(1)设小明速度是x米/分,则小明父亲的速度是4x米/分.
∵由图象可得:10x+40x=4400-400,
解得:x=80,
则10x=800,
∴B(10,1200).
设直线AB解析式为y=kx+b(k≠0)
∵A(0,4400),B(10,1200)
∴
,
解得:
,
所以直线AB解析式为:y=-320x+4400;
(2)∵10+
=22.5>20,
∴小明在比赛开始前不能到达体育场.由
=10,得n=1.5
∴若想在规定时间到达体育场至少以原来速度的1.5倍返回才可以.
∵由图象可得:10x+40x=4400-400,
解得:x=80,
则10x=800,
∴B(10,1200).
设直线AB解析式为y=kx+b(k≠0)
∵A(0,4400),B(10,1200)
∴
|
解得:
|
所以直线AB解析式为:y=-320x+4400;
(2)∵10+
| 1200 |
| 1.2×80 |
∴小明在比赛开始前不能到达体育场.由
| 1200 |
| 80n |
∴若想在规定时间到达体育场至少以原来速度的1.5倍返回才可以.
点评:本题考查了一次函数的应用.解题时,要学生具备一定的读图能力.

练习册系列答案
相关题目
下列图形一定有外接圆的是( )
| A、三角形 | B、平行四边形 |
| C、梯形 | D、菱形 |
下列各数:
,
,0.45,0,-
,9.181181118,其中无理数有( )
| 5 |
| π |
| 2 |
| 3 | 0.001 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.
将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF. 为了开发利用海洋资源,需要测量某岛屿的两端A、B的距离,如图,勘测飞机在距海平面垂直距离为100米的点C处测得点A的俯角为60°,然后沿着平行于AB的方向飞行了500米至D处,在D处测得点B的俯角为45°,求岛屿两端A、B的距离.(结果精确到0.1米)说明:①A、B、C、D在与海平面垂直的同一平面上;②参考数据:
为了开发利用海洋资源,需要测量某岛屿的两端A、B的距离,如图,勘测飞机在距海平面垂直距离为100米的点C处测得点A的俯角为60°,然后沿着平行于AB的方向飞行了500米至D处,在D处测得点B的俯角为45°,求岛屿两端A、B的距离.(结果精确到0.1米)说明:①A、B、C、D在与海平面垂直的同一平面上;②参考数据:
 做大小两个长方体纸盒,长、宽、高的尺寸如图所示(单位:cm):
做大小两个长方体纸盒,长、宽、高的尺寸如图所示(单位:cm): 已知抛物线y=ax2+bx+c与x轴相交于点A(
已知抛物线y=ax2+bx+c与x轴相交于点A(