题目内容
 如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.求:
如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.求:(1)桥拱的半径.
(2)现有一轮船宽60米,船舱顶部为长方形并高出水面9米要经过这里,这艘轮船能顺利通过吗?
考点:垂径定理的应用,勾股定理
专题:
分析:(1)根据垂径定理和勾股定理求解;
(2)连接EM,设MD=30米,可求得此时DE的高,即可求得DF的长,比较9米,即可得到此时货船能顺利通过这座拱桥.
(2)连接EM,设MD=30米,可求得此时DE的高,即可求得DF的长,比较9米,即可得到此时货船能顺利通过这座拱桥.
解答: 解:(1)如图,点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
解:(1)如图,点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
则由垂径定理知,点F是AB的中点,AF=FB=
AB=40,EF=ED-FD=AE-DF,
由勾股定理知,AE2=AF2+EF2=AF2+(AE-DF)2,
设圆的半径是r,
则:r2=402+(r-20)2,
解得:r=50;
(2)如图,货船能顺利通过这座拱桥.理由:
连接EM,设MD=30米.
∵DE⊥MN,EF=50-20=30(m),
在Rt△DEM中,DE=
=40(米),
∵DF=DE-EF=40-30=10(米)
∵10米>9米,
∴货船能顺利通过这座拱桥.
 解:(1)如图,点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
解:(1)如图,点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,则由垂径定理知,点F是AB的中点,AF=FB=
| 1 |
| 2 |
由勾股定理知,AE2=AF2+EF2=AF2+(AE-DF)2,
设圆的半径是r,
则:r2=402+(r-20)2,
解得:r=50;
(2)如图,货船能顺利通过这座拱桥.理由:

连接EM,设MD=30米.
∵DE⊥MN,EF=50-20=30(m),
在Rt△DEM中,DE=
| EM2-DM2 |
∵DF=DE-EF=40-30=10(米)
∵10米>9米,
∴货船能顺利通过这座拱桥.
点评:此题考查了垂径定理的应用.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
下列事件是随机事件的是( )
| A、通常加热到100℃时,水沸腾 |
| B、篮球队员在罚球线上投篮一次,未投中 |
| C、度量三角形内角和,结果是360° |
| D、掷一个质地均匀的正方体骰子,向上的一面出现的点数大于0 |
下列调查中,适宜采用全面调查(普查)方式的是( )
| A、调查全国青少年儿童的睡眠时间 |
| B、调查本班50名同学的身高情况 |
| C、调查我市居民的年人均消费 |
| D、调查某日光灯管厂一批灯管的使用寿命 |
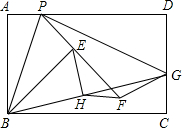 在远古时代,我们的祖先就发现并证明了在直角三角形中斜边上中线等于斜边的一半,今天的我们可以直接运用.现有一张长方形纸片ABCD,在AD边上任取一点P(不与点A、点D重合),以BP所在直线为折痕,将长方形如图翻折,使A点翻到E点,再将PD翻到与PE所在直线位置重合,得到折痕PG,PG与DC边交于点G,点D翻到点F处,如图,连接BG,取BG的中点H,连接HE、HF,试猜想线段HE与HF之间的大小关系,并说明理由.
在远古时代,我们的祖先就发现并证明了在直角三角形中斜边上中线等于斜边的一半,今天的我们可以直接运用.现有一张长方形纸片ABCD,在AD边上任取一点P(不与点A、点D重合),以BP所在直线为折痕,将长方形如图翻折,使A点翻到E点,再将PD翻到与PE所在直线位置重合,得到折痕PG,PG与DC边交于点G,点D翻到点F处,如图,连接BG,取BG的中点H,连接HE、HF,试猜想线段HE与HF之间的大小关系,并说明理由. 现有一张演唱会的票,小明和小亮两人都想去.于是两想了个办法.用如图所示的两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成3等分,每份分别标有1,3,6这三个数字;转盘B被均匀地分成4等分,每份分别标有2,4,5,7这四个数字.①同时自由转动转盘A和B;②转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积为偶数,小明去,否则小亮去.这个方法公平吗?请你说明理由.若不公平,请你帮忙修改一个公平的规则.
现有一张演唱会的票,小明和小亮两人都想去.于是两想了个办法.用如图所示的两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成3等分,每份分别标有1,3,6这三个数字;转盘B被均匀地分成4等分,每份分别标有2,4,5,7这四个数字.①同时自由转动转盘A和B;②转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积为偶数,小明去,否则小亮去.这个方法公平吗?请你说明理由.若不公平,请你帮忙修改一个公平的规则.