题目内容
16.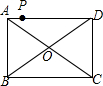 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )| A. | 4.8 | B. | 5 | C. | 6 | D. | 7.2 |
分析 首先连接OP,由矩形的两条边AB、BC的长分别为6和8,可求得OA=OD=5,△AOD的面积,然后由S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+OD•PF求得答案.
解答 解:连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB•BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=$\frac{1}{2}$S矩形ABCD=24,
∴S△AOD=$\frac{1}{2}$S△ACD=12,
∵S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+$\frac{1}{2}$OD•PF=$\frac{1}{2}$×5×PE+$\frac{1}{2}$×5×PF=$\frac{5}{2}$(PE+PF)=12,
解得:PE+PF=4.8.
故选:A.
点评 此题考查了矩形的性质以及三角形面积问题.此题难度适中,注意掌握辅助线的作法以及掌握整体数学思想的运用是解题的关键.

练习册系列答案
相关题目
7.学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数$\overline{x}$(单位:分)及方差s2如表所示:
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 7 | 8 | 8 | 7 |
| s2 | 1 | 1.2 | 1 | 1.8 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
4.一元二次方程2x2-3x+1=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
8.不等式$\frac{x+1}{2}$>$\frac{2x+2}{3}$-1的正整数解的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论: