题目内容
1. 如图,在小山的东侧A点处有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C点处,此时热气球上的人测得小山西侧B点的俯角为30°,求小山东西两侧A、B两点间的距离.
如图,在小山的东侧A点处有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C点处,此时热气球上的人测得小山西侧B点的俯角为30°,求小山东西两侧A、B两点间的距离.
分析 过点A作AD⊥BC,垂足为D,在直角△ACD中利用三角函数求得AD的长,然后在直角△ABD中利用三角函数求得AB的长.
解答  解:如图,过点A作AD⊥BC,垂足为D,
解:如图,过点A作AD⊥BC,垂足为D,
∵在Rt△ACD中,∠ACD=75°-30°=45°,
AC=30×25=750(米),
∴AD=AC•sin45°=375$\sqrt{2}$(米).
在Rt△ABD中,
∵∠B=30°,
∴AB=2AD=750$\sqrt{2}$(米).
所以小山东西两侧A、B两点间的距离为750$\sqrt{2}$米.
点评 本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 某校对学生上学方式进行了一次抽样调查,如图是根据此次调查结果所绘制的一个未完成的扇形统计图,已知该校学生共有2000人,被调查的学生中乘车的有9人,则下列四种说法中,错误的是( )
某校对学生上学方式进行了一次抽样调查,如图是根据此次调查结果所绘制的一个未完成的扇形统计图,已知该校学生共有2000人,被调查的学生中乘车的有9人,则下列四种说法中,错误的是( )
 某校对学生上学方式进行了一次抽样调查,如图是根据此次调查结果所绘制的一个未完成的扇形统计图,已知该校学生共有2000人,被调查的学生中乘车的有9人,则下列四种说法中,错误的是( )
某校对学生上学方式进行了一次抽样调查,如图是根据此次调查结果所绘制的一个未完成的扇形统计图,已知该校学生共有2000人,被调查的学生中乘车的有9人,则下列四种说法中,错误的是( )| A. | 被调查的学生有60人 | |
| B. | 被调查的学生中,步行的有27人 | |
| C. | 估计全校骑车上学的学生有700人 | |
| D. | 扇形图中,乘车部分所对应的圆心角为15° |
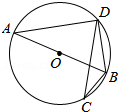 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD=40°.
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD=40°.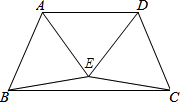 如图,△ABE与△CDE是两个全等的等边三角形,且EA⊥ED.有下列四个结论:(1)∠EBC=15°;(2)AD∥BC;(3)直线CE与AB垂直;(4)四边形ABCD是轴对称图形.其中正确的结论有( )
如图,△ABE与△CDE是两个全等的等边三角形,且EA⊥ED.有下列四个结论:(1)∠EBC=15°;(2)AD∥BC;(3)直线CE与AB垂直;(4)四边形ABCD是轴对称图形.其中正确的结论有( ) 把4个正方体摆放成如图所示的几何体,该几何体的俯视图是( )
把4个正方体摆放成如图所示的几何体,该几何体的俯视图是( )


