题目内容
若a、b、c是三角形的三边,且满足关系式a2-2bc=c2-2ab,试判断这个三角形的形状.
考点:因式分解的应用
专题:计算题
分析:已知等式变形后,利用完全平方公式及平方差公式分解,得到a=c,即可确定出三角形形状.
解答:解:把a2-2bc=c2-2ab,变形得:a2+2ab+b2-(b2+2bc+c2)=0,
即(a+b)2-(b+c)2=0,即(a+2b+c)(a-c)=0,
可得a=c,
则这个三角形为等腰三角形.
即(a+b)2-(b+c)2=0,即(a+2b+c)(a-c)=0,
可得a=c,
则这个三角形为等腰三角形.
点评:此题考查了因式分解的应用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在下列的代数式的写法中,表示正确的一个是( )
| A、“负x的平方”记作-x2 | ||||
| B、“x的3倍”记作x3 | ||||
C、“a除以2b的商”记作
| ||||
D、“y与1
|
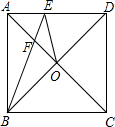 如图,正方形ABCD的边长为2,连接对角线AC、BD交于点O,∠ABD的角平分线交AC于点F,交AD于点E,连接OE,则△OEF的面积为( )
如图,正方形ABCD的边长为2,连接对角线AC、BD交于点O,∠ABD的角平分线交AC于点F,交AD于点E,连接OE,则△OEF的面积为( )A、
| ||||
B、
| ||||
C、3-2
| ||||
D、2
|

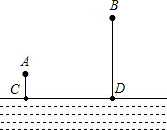 如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km.现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20 000元/千米.
如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km.现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20 000元/千米. 已知:如图,正方形ABCD的边长我3,点E在BC上,CE=2BE,将正方形折叠,使点A与点E重合,折痕为MN,交AE于点G.求△ANE的面积.
已知:如图,正方形ABCD的边长我3,点E在BC上,CE=2BE,将正方形折叠,使点A与点E重合,折痕为MN,交AE于点G.求△ANE的面积.