题目内容
已知两组数x1,x2,…,xn和y1,y2,…,yn的平均数分别是 和
和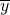 ,那么一组新数据8x1,8x2,…,8xn的平均数是________;另一组新数据x1+y1,x2+y2,…,xn+yn的平均数是________.
,那么一组新数据8x1,8x2,…,8xn的平均数是________;另一组新数据x1+y1,x2+y2,…,xn+yn的平均数是________.
8

分析:根据平均数的公式: 的变形,可求解.
的变形,可求解.
解答:∵x1,x2,…,xn和y1,y2,…,yn的平均数分别是 和
和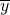 ,
,
∴x1+x2+…+xn=n ,y1+y2+…+yn=n
,y1+y2+…+yn=n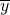 ,
,
∴新数据8x1,8x2,…,8xn的平均数=(8x1+8x2+…+8xn)÷n=8n ÷n=8
÷n=8 ,
,
新数据x1+y1,x2+y2,…,xn+yn的平均数=(x1+y1+x2+y2+…+xn+yn)÷n=(x1+x2+…+xn+y1+y2+…+yn)÷n= .
.
故答案 .
.
点评:熟练掌握平均数的计算公式及其变形,此题可作为结论记住.


分析:根据平均数的公式:
 的变形,可求解.
的变形,可求解.解答:∵x1,x2,…,xn和y1,y2,…,yn的平均数分别是
 和
和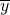 ,
,∴x1+x2+…+xn=n
 ,y1+y2+…+yn=n
,y1+y2+…+yn=n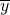 ,
,∴新数据8x1,8x2,…,8xn的平均数=(8x1+8x2+…+8xn)÷n=8n
 ÷n=8
÷n=8 ,
,新数据x1+y1,x2+y2,…,xn+yn的平均数=(x1+y1+x2+y2+…+xn+yn)÷n=(x1+x2+…+xn+y1+y2+…+yn)÷n=
 .
.故答案
 .
.点评:熟练掌握平均数的计算公式及其变形,此题可作为结论记住.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目