题目内容

2．不论a，b取何有理数，a2+b2-8a+14b+75的值必是（　　）
A．正数B．零C．负数D．非负数

分析 直接利用完全平方公式将原式变形进而利用偶次方的性质判断得出答案．

解答 解：a2+b2-8a+14b+75
=（a2-8a+16）+（b2+14b+49）+10
=（a-4）2+（b+7）2+10，
∵（a-4）2≥0，（b+7）2≥0，
∴（a-4）2+（b+7）2+10＞0，
∴不论a，b取何有理数，a2+b2-8a+14b+75的值必是正数．
故选：A．

点评 此题主要考查了因式分解的应用以及偶次方的性质，正确应用完全平方公式是解题关键．

练习册系列答案
相关题目
5．（1）如图1，已知E是矩形ABCD的边AB上一点，EF⊥DE交BC于点F，证明：△ADE∽△BEF．
这个相似的基本图形像字母K，可以称为“K”型相似，但更因为图形的结构特征是一条线上有3个垂直关系，也常被称为“一线三垂直”，那普通的3个等角又会怎样呢？
（2）变式一如图2，已知等边三角形ABC，点D、E分别为BC，AC上的点，∠ADE=60°．
①图中有相似三角形吗？请说明理由．
②如图3，若将∠ADE在△ABC的内部（∠ADE两边不与BC重合），绕点D逆时针旋转一定的角度，还有相似三角形吗？△BDF∽△CED（若有请写出相似三角形，没有则填“无”）
（3）变式二如图4，隐藏变式1图形中的线段AE，在得到的新图形中．
①如果∠B=∠C=∠ADE=50°，图中有相似三角形吗？请说明理由．
②如图5，若∠B=∠C=∠ADE=∠a，∠a为任意角，还有相似三角形吗？△ABD∽△DCE．（若有请写出相似三角形，没有则填“无”）
（4）变式三，已知，相邻两条平行直线间的距离相等，若等腰直角△ABC的三个顶点分别在这三条平行直线上，则cosa的值是$\frac{3\sqrt{10}}{10}$（直接写出结果）．
13．解方程：
①x2-6x+8=0
②（x-6）2=x-6．
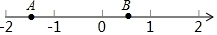10．如图，一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B，点A表示-1$\frac{1}{2}$，设点B所表示的数为m
（1）求m的值；
（2）求|m-1|+（m-6）的值．
17．小明饶着一个五边形的花圃走了一圈，他一共转了多少度（　　）
A．180°B．360°C．540°D．720°
7．已知：A=-2ab，B=3（a-b），求A•B．
14．尺规作图：（不写作法，保留作图痕迹）．

（1）如图1，已知：点A和直线l．求作：点A′，使点A′和点A关于直线l对称．
（2）某学校正在进行校园环境的改造工程设计，准备在校内一块四边形花坛内栽上一棵桂花树．如图2，要求：
①桂花树的位置（视为点P），到花坛的两边AB、BC的距离相等；
②点P到点A、D的距离也相等．请用尺规作图作出栽种桂花树的位置点P．
11．观察：$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=（$\frac{1}{1}$-$\frac{1}{2}$）+（$\frac{1}{2}$-$\frac{1}{3}$）+（$\frac{1}{3}$-$\frac{1}{4}$）=1-$\frac{1}{4}$=$\frac{3}{4}$
（1）计算$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{9×10}$
（2）计算$\frac{3}{1×2}$+$\frac{3}{2×3}$+$\frac{3}{3×4}$+…+$\frac{3}{n×（n+1）}$
（3）拓展应用：①解方程：$\frac{1}{（x-4）（x-3）}$+$\frac{1}{（x-3）（x-2）}$+$\frac{1}{（x-2）（x-1）}$+$\frac{1}{（x-1）x}$+$\frac{1}{x（x+1）}$=0
②计算$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×10}$+$\frac{1}{10×13}$+$\frac{1}{13×16}$．
12．下列函数哪些是正比例函数？是正比例函数的指出比例系数．
（1）y=-4x   （2）y=3x-1   （3）y=$\frac{5x}{6}$    （4）y=$\frac{9}{x}$     （5）y=-0.9x     （6）y=（$\sqrt{5}$-1）x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网