题目内容
4.已知直角坐标平面内的点A(1,4)到原点的距离等于$\sqrt{17}$.分析 作AB⊥x轴于B,则∠ABO=90°,OB=1,AB=4,由勾股定理求出AO即可.
解答 解:作AB⊥x轴于B,如图所示:
则∠ABO=90°,OB=1,AB=4,
∴AO=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$;
即点A(1,4)到原点的距离等于$\sqrt{17}$;
故答案为:$\sqrt{17}$.
点评 本题考查了勾股定理、坐标与图形性质;熟练掌握勾股定理,由勾股定理求出AO是解决问题的关键.

练习册系列答案
相关题目
15.下列能判定两个三角形全等的是( )
①三条边对应相等;②三个角对应相等;③两边和一个角对应相等;
④两角和它们的夹边对应相等;⑤两角和一个角的对边对应相等.
①三条边对应相等;②三个角对应相等;③两边和一个角对应相等;
④两角和它们的夹边对应相等;⑤两角和一个角的对边对应相等.
| A. | ①②③ | B. | ①③⑤ | C. | ②③④ | D. | ①④⑤ |
19.数据1 460 000 000用科学记数法表示应是( )
| A. | 146×107 | B. | 1.46×109 | C. | 1.46×1010 | D. | 0.146×1010 |
13.课外阅读课上,老师将一批书分给各小组,若每小组8本,还剩余3本;若每小组9本,则还缺2本,问有几个小组?若设有x个小组,则依题意列方程为( )
| A. | 8x-3=9x+2 | B. | 8x+3=9x-2 | C. | 8(x-3)=9(x+2) | D. | 8(x+3)=9(x-2) |
2.若a2的算术平方根是4,则a为( )
| A. | 16 | B. | 4 | C. | ±2 | D. | ±4 |
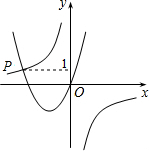 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P(-3,1),则关于x的不等式ax2+bx>-$\frac{3}{x}$的解为x<-3或x>0.
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P(-3,1),则关于x的不等式ax2+bx>-$\frac{3}{x}$的解为x<-3或x>0. 如图.已知AB=AC,∠ACD=∠ABD,试问∠ADB与∠BDC之间有怎样的数量关系?并证明你所得的结论.
如图.已知AB=AC,∠ACD=∠ABD,试问∠ADB与∠BDC之间有怎样的数量关系?并证明你所得的结论.