题目内容
6.已知n>1,M=$\frac{n}{n-1}$,N=$\frac{n-1}{n}$,P=$\frac{n}{n+1}$,则M、N、P的大小关系( )| A. | M>N>P | B. | M>P>N | C. | P>N>M | D. | P>M>N |
分析 利用作差法比较大小即可.
解答 解:∵n>1,M=$\frac{n}{n-1}$,N=$\frac{n-1}{n}$,P=$\frac{n}{n+1}$,
∴M-N=$\frac{n}{n-1}$-$\frac{n-1}{n}$=$\frac{{n}^{2}-{n}^{2}+2n+1}{n(n-1)}$=$\frac{2n+1}{n(n-1)}$>0,即M>N,
N-P=$\frac{n-1}{n}$-$\frac{n}{n+1}$=$\frac{{n}^{2}-1-{n}^{2}}{n(n+1)}$=-$\frac{1}{n(n+1)}$<0,即N<P,
M-P=$\frac{n}{n-1}$-$\frac{n}{n+1}$=$\frac{2n}{(n+1)(n-1)}$>0,即M>P,
则M>P>N.
故选B.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
17.某果品公司欲请汽车运输公司或火车货运站将一批水果从A地运到B地,已知汽车和火车从A地运到B地的运输路程均为x(x>0)千米,若这批水果在运输过程中(含装卸时间)的损耗都为180元/时,要收取的其他费用及有关运输资料由下表给出:
(1)请你分别用含x的代数式表示用汽车运输所需总费用M(元)和用火车运输所需总费用N(元);
(2)当A、B两地路程为600千米时,那么你认为采用哪种运输工具比较好(即运输所需总费用较少)?
| 运输工具 | 途中平均速度 (单位:千米/时) | 途中平均费用 (单位:元/千米) | 装卸时间 (单位:小时) | 装卸费用 (单位:元) |
| 汽车 | 60 | 8 | 2 | 1500 |
| 火车 | 100 | 6 | 4 | 2400 |
(2)当A、B两地路程为600千米时,那么你认为采用哪种运输工具比较好(即运输所需总费用较少)?
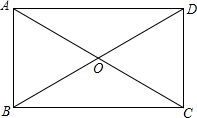 已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.求证:
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.求证: 某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?
某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?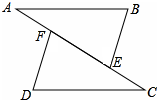 如图,点A、F、E、C在同一条直线上,AF=CE,BE=DF,AB=CD,求证:AB∥CD.
如图,点A、F、E、C在同一条直线上,AF=CE,BE=DF,AB=CD,求证:AB∥CD.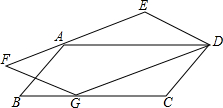 如图,ABCD是一个平行四边形,其面积等于8平方厘米,另一个平行四边形DEFG,EF过A点,G在BC上.问:平行四边形DEFG的面积是多少平方厘米?
如图,ABCD是一个平行四边形,其面积等于8平方厘米,另一个平行四边形DEFG,EF过A点,G在BC上.问:平行四边形DEFG的面积是多少平方厘米?