题目内容
9．如果矩形ABCD的对角线的交点与平面直角坐标系的原点重合，且点A和点B的坐标分别为（3，2）和（-3，2），则矩形的面积为（ ）| A． | 32 | B． | 24 | C． | 6 | D． | 8 |
分析 从题意可知AB和x轴平行，且矩形ABCD的对角线的交点与平面直角坐标系的原点重合，所以AB=6，BC=4．
解答 解：因为A和点B的坐标分别为（-3，2）和（3，2），且矩形ABCD的对角线的交点与平面直角坐标系的原点重合
所以AB=6，BC=4，
所以矩形的面积为6×4=24．
故选B．
点评 本题考查矩形的性质、矩形的面积以及坐标与图形的性质，解决问题的关键是根据顶点的坐标得出矩形的边长．
练习册系列答案
相关题目
19．平面内一点P离⊙O上的点最近距离为5cm，离⊙O上的点最远距离为13cm，则⊙O的半径为（ ）
| A． | 4cm | B． | 4或9cm | C． | 8cm | D． | 8或18cm |
如图，△ABC≌△ADE，BC的延长线交DA于F，交DE于G，∠D=25°，∠E=115°，∠DAC=30°，求∠DGB的度数65°．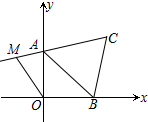
如图所示，在平面直角坐标系中，A（0，3）、B（3，0）、C（4，4），线段CA的延长线上有一点M，使四边形ABOM的面积与三角形ABC的面积相等，则M的坐标为（-2，$\frac{5}{2}$）．
14．
如图，与∠5是同旁内角的是（ ）
如图，与∠5是同旁内角的是（ ）| A． | ∠1 | B． | ∠2 | C． | ∠3 | D． | ∠4 |
有理数a、b、c在数轴上的位置如图所示，其中O是原点，|b|=|c|．