题目内容
当m为何正整数时，关于x的一元二次方程x2-2（m-2）x+m2-4m-5=0的两个实数根都小于3？
考点：一元二次方程根的分布
专题：
分析：首先将方程因式分解求得方程的两根，利用两个实数根都小于3列出不等式求得m的取值范围即可．
解答：解：∵方程因式分解：x2-2（m-2）x+（m-5）（m+1）=0，
∴（x-m-1）（x-m+5）=0
得：x1=m+1，x2=m-5
∵两实根都小于3，
∴
，
即m＜2，且m＜8
综合得：m＜2．
∴（x-m-1）（x-m+5）=0
得：x1=m+1，x2=m-5
∵两实根都小于3，
∴
|
即m＜2，且m＜8
综合得：m＜2．
点评：本题考查了一元二次方程的根的分布，解题的关键是将一元二次方程因式分解，难度不是很大．
练习册系列答案
相关题目
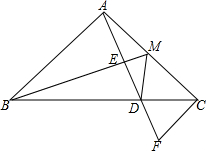已知如图，在△ABC中，∠BAC=90°，AB=AC，M是AC边的中点，AD⊥BM交BC于D，交BM于E，CF⊥AC，证明：