题目内容
 如图所示,在正方形ABCD中,E是BC上的点连接AE.作BF⊥AE垂足为H,交CD于F作CG∥AE,交BF于G.求证:
如图所示,在正方形ABCD中,E是BC上的点连接AE.作BF⊥AE垂足为H,交CD于F作CG∥AE,交BF于G.求证:(1)CG=BH;
(2)FC2=BF•GF.
考点:正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质
专题:证明题
分析:(1)根据正方形的性质可得AB=BC,再利用同角的余角相等求出∠BAH=∠CBG,再利用“角角边”证明△ABH和△BCG全等,根据全等三角形对应边相等可得CG=BH;
(2)利用两组角对应相等,两三角形相似求出△BCF和△CGF相似,然后根据相似三角形对应边成比例列式整理即可得证.
(2)利用两组角对应相等,两三角形相似求出△BCF和△CGF相似,然后根据相似三角形对应边成比例列式整理即可得证.
解答:证明:(1)在正方形ABCD中,AB=BC,∠ABC=90°,
∴∠ABH+∠CBG=90°,
∵BF⊥AE,
∴∠BAH+∠ABH=90°,
∴∠BAH=∠CBG,
在△ABH和△BCG中,
,
∴△ABH≌△BCG(AAS),
∴CG=BH;
(2)∵BF⊥AE,CG∥AE,
∴CG⊥BF,
∵∠BFC=∠CFG,∠BCD=∠CGF=90°,
∴△BCF∽△CGF,
∴
=
,
∴FC2=BF•GF.
∴∠ABH+∠CBG=90°,
∵BF⊥AE,
∴∠BAH+∠ABH=90°,
∴∠BAH=∠CBG,
在△ABH和△BCG中,
|
∴△ABH≌△BCG(AAS),
∴CG=BH;
(2)∵BF⊥AE,CG∥AE,
∴CG⊥BF,
∵∠BFC=∠CFG,∠BCD=∠CGF=90°,
∴△BCF∽△CGF,
∴
| FC |
| GF |
| BF |
| FC |
∴FC2=BF•GF.
点评:本题考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质,(1)熟记各性质并求出三角形全等是解题的关键,(2)确定出CG⊥BF并求出三角形相似是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 已知,AB是⊙O的直径,弦CD⊥AB,E是
已知,AB是⊙O的直径,弦CD⊥AB,E是
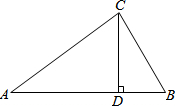 如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,DC=12.
如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,DC=12.