题目内容
如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于点E，AC=6，AB=10，则BE=考点：角平分线的性质,全等三角形的判定与性质
专题：几何图形问题
分析：根据角平分线上的点到角的两边距离相等可得CD=DE，再利用“HL”证明Rt△ACD和Rt△AED全等，根据全等三角形对应边相等可得AE=AC，然后根据BE=AB-AE计算即可得解．
解答：解：∵AD平分∠BAC，∠C=90°，DE⊥AB，
∴CD=DE，
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴AE=AC=6，
∴BE=AB-AE=10-6=4．
故答案为：4．
∴CD=DE，
在Rt△ACD和Rt△AED中，
|
∴Rt△ACD≌Rt△AED（HL），
∴AE=AC=6，
∴BE=AB-AE=10-6=4．
故答案为：4．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记性质并求出两三角形全等是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
将一张长方形纸片如图方式折叠，BD、BE为折痕，若∠ABE=15°，则∠DBC=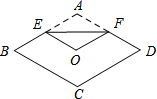
如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称中心O处，折痕为EF．若菱形ABCD的边长为4cm，∠A=120°，则EF=
如图是一个围棋棋盘的局部，若把这个围棋棋盘放置在一个平面直角坐标系中，白棋①的坐标是（-3，-1），白棋③的坐标是（-2，-3），则黑棋②的坐标是