题目内容
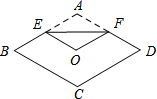 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为4cm,∠A=120°,则EF=
如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为4cm,∠A=120°,则EF=考点:菱形的性质,翻折变换(折叠问题)
专题:
分析:根据菱形性质得出AC⊥BD,AC平分∠BAD,求出∠ABO=30°,求出AO,BO、DO,根据折叠得出EF⊥AC,EF平分AO,推出EF∥BD,推出,EF为△ABD的中位线,根据三角形中位线定理求出即可.
解答: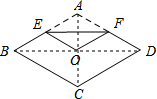 解:连接BD、AC,
解:连接BD、AC,
∵四边形ABCD是菱形,
∴AC⊥BD,AC平分∠BAD,
∵∠BAD=120°,
∴∠BAC=60°,
∴∠ABO=90°-60°=30°,
∵∠AOB=90°,
∴AO=
AB=
×4=2(cm),
由勾股定理得:BO=DO=2
(cm),
∴BD=4
(cm),
∵A沿EF折叠与O重合,
∴EF⊥AC,EF平分AO,
∵AC⊥BD,
∴EF∥BD,
∴EF为△ABD的中位线,
∴EF=
BD=2
(cm),
故答案为:2
.
 解:连接BD、AC,
解:连接BD、AC,∵四边形ABCD是菱形,
∴AC⊥BD,AC平分∠BAD,
∵∠BAD=120°,
∴∠BAC=60°,
∴∠ABO=90°-60°=30°,
∵∠AOB=90°,
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得:BO=DO=2
| 3 |
∴BD=4
| 3 |
∵A沿EF折叠与O重合,
∴EF⊥AC,EF平分AO,
∵AC⊥BD,
∴EF∥BD,
∴EF为△ABD的中位线,
∴EF=
| 1 |
| 2 |
| 3 |
故答案为:2
| 3 |
点评:本题考查了折叠性质,菱形性质,含30度角的直角三角形性质,勾股定理,平行线分线段成比例定理等知识点的应用,主要考查学生综合运用定理进行推理和计算的能力.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 某高校图书馆整理图书,把图书馆内的书分成三类,A.表示科技类,B.表示哲学类,C.表示艺术类,所占的百分比如图所示,如果该校图书馆共有8500册,则艺术类图书馆共有
某高校图书馆整理图书,把图书馆内的书分成三类,A.表示科技类,B.表示哲学类,C.表示艺术类,所占的百分比如图所示,如果该校图书馆共有8500册,则艺术类图书馆共有 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,AC=6,AB=10,则BE=
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,AC=6,AB=10,则BE= 如图是正方体的展开图,则原正方体相对两个面上的数字和最小的是
如图是正方体的展开图,则原正方体相对两个面上的数字和最小的是 如图,边长为1的小正方形构成的网格中,⊙O的半径为1,则图中阴影部分两个小扇形的面积之和为
如图,边长为1的小正方形构成的网格中,⊙O的半径为1,则图中阴影部分两个小扇形的面积之和为