题目内容
15.下列四个多项式中为完全平方式的为( )| A. | 4a2+2ab+b2 | B. | m2+2mn+n2 | C. | m2n2-mn+1 | D. | 4x2+10x+25 |
分析 根据完全平方公式:(a±b)2=a2±2ab+b2进行分析.
解答 解:A、4a2+4ab+b2=(2a+b)2,错误;
B、m2+2mn+n2=(m+n)2,正确;
C、m2n2-2mn+1=(mn-1)2,错误;
D、4x2+20x+25=(2x+5)2,错误;
故选B
点评 本题考查了完全平方式,关键是根据两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式分析.

练习册系列答案
相关题目
10.一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售(整箱配货),预计每箱水果的盈利情况如下表:
(1)如果按照“甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱”的方案配货,请你计算出经销商能盈利多少元?
(2)如果按照“甲、乙两店盈利相同配货”的方案配货,请写出一种配货方案:A种水果甲店2箱,乙店8箱;B种水果甲店6箱,乙店4箱,并根据你填写的方案计算出经销商能盈利多少元?
(3)在甲、乙两店各配货10箱,且保证乙店盈利不小于115元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少元?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
(2)如果按照“甲、乙两店盈利相同配货”的方案配货,请写出一种配货方案:A种水果甲店2箱,乙店8箱;B种水果甲店6箱,乙店4箱,并根据你填写的方案计算出经销商能盈利多少元?
(3)在甲、乙两店各配货10箱,且保证乙店盈利不小于115元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少元?
4.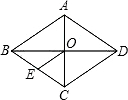 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
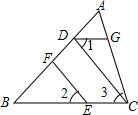 如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,
如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB, 如图都是小方格,A,B,C构成三角形,则cosA=$\frac{3}{5}$.
如图都是小方格,A,B,C构成三角形,则cosA=$\frac{3}{5}$.