题目内容
11.关于x的方程mx2-(m+2)x+$\frac{m}{4}$=0有两个实数根.(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求m的值;若不存在,说明理由.
分析 (1)根据方程有两个实数根,得到根的判别式大于等于0,列出关于m的不等式,求出不等式的解集,即可得到m的范围;
(2)假设存在,然后利用根的判别式求得m的值,根据m的值是否能使得一元二次方程有实数根作出判断即可.
解答 解:(1)∵关于x的方程mx2-(m+2)x+$\frac{m}{4}$=0有两个实数根,
∴△=b2-4ac=(m+1) 2-4m•$\frac{m}{4}$≥0,
解得:m≥-$\frac{1}{2}$,
则m的取值范围是m≥-$\frac{1}{2}$且m≠0.
故答案为:m≥-$\frac{1}{2}$且m≠0;
(2)不存在符合条件的实数m.
设方程两根为x1,x2则x1+x2=$\frac{m+2}{m}$,x1•x2=$\frac{1}{4}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{4(m+2)}{m}$=0,
解得m=-2,此时△<0,
∴原方程无解,故不存在.
点评 此题主要考查了一元二次方程的判别式和根与系数的关系,解题时将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
19.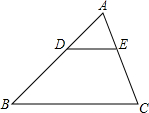 如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )
如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )
 如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )
如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )| A. | 1:2 | B. | 1:4 | C. | 1:25 | D. | $\sqrt{5}$:5 |
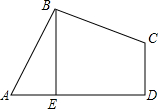 如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE=( )
如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE=( )
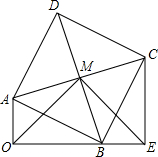 如图,以Rt△OAB的斜边AB为边作正方形ABCD,CE⊥OB交OB延长线于E,对角线AC,BD交于点M,连OM.
如图,以Rt△OAB的斜边AB为边作正方形ABCD,CE⊥OB交OB延长线于E,对角线AC,BD交于点M,连OM.
 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上,若AD=4,BE=1,求:
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上,若AD=4,BE=1,求: