题目内容
20.如图,点O是△ABC的内心,根据下列条件,求∠BOC的度数.(1)∠ABC=50°,∠ACB=60°;
(2)∠A=50°.

分析 (1)由点O是△ABC的内心,得出OB平分∠ABC,OC平分∠ACB,得出∠OBC、∠OCB的度数,再由三角形内角和即可得出∠BOC的度数;
(2)由三角形内角和定理求出∠ABC+∠ACB=130°,由点O是△ABC的内心,得出OB平分∠ABC,OC平分∠ACB,得出∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=65°,由三角形内角和定理求出∠BOC的度数即可.
解答 解:(1)∵点O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC=25°,∠OCB=$\frac{1}{2}$∠ACB=30°,
∴∠BOC=180°-∠OBC-∠OCB=180°-25°-30°=125°;
(2)∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,
∵点O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=65°,
∴∠BOC=180°-∠OBC-∠OCB=180°-(∠OBC+∠OCB)=115°.
点评 本题考查了三角形内切圆与内心、三角形内角和定理;熟练掌握三角形的内心和三角形内角和定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
11.关于x的方程mx2-(m+2)x+$\frac{m}{4}$=0有两个实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求m的值;若不存在,说明理由.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求m的值;若不存在,说明理由.
8. 如图,下面几何图形的俯视图是( )
如图,下面几何图形的俯视图是( )
 如图,下面几何图形的俯视图是( )
如图,下面几何图形的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5. 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )| A. | $\widehat{AC}$ | B. | $\widehat{AD}$ | C. | $\widehat{ACD}$ | D. | $\widehat{ADB}$ |
 如图,在△ABC中,点D、E分别为边AC、AB上的点,且∠ADE=∠B,AE=3,BE=4,则AD•AC=21.
如图,在△ABC中,点D、E分别为边AC、AB上的点,且∠ADE=∠B,AE=3,BE=4,则AD•AC=21.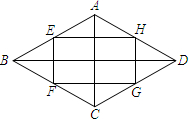 如图,顺次连接菱形ABCD的各边中点E,F,G,H,若AC=6,BD=12,则四边形EFGH的面积为18.
如图,顺次连接菱形ABCD的各边中点E,F,G,H,若AC=6,BD=12,则四边形EFGH的面积为18.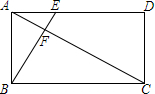 如图,在矩形ABCD中,AB=4cm,AD=8cm,点E在边AD上,AE:ED=1:3,AC、BE交于点F.
如图,在矩形ABCD中,AB=4cm,AD=8cm,点E在边AD上,AE:ED=1:3,AC、BE交于点F.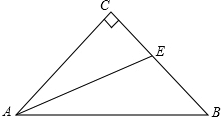 如图,等腰△ABC中,∠ACB=90°,I为△ABC的内心,AI的延长线交BC于E.若IE=1,则AI=1+$\sqrt{2}$.
如图,等腰△ABC中,∠ACB=90°,I为△ABC的内心,AI的延长线交BC于E.若IE=1,则AI=1+$\sqrt{2}$.