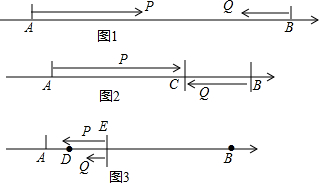
题目内容
数轴上(图1),A、B两点表示的数分别是a、b,且|a+7|+(3a+b)2=0;P、Q分别从A、B同时出发,在A、B之间做往返运动,其速度分别记为VP和VQ,VP>VQ;
(1)求a、b的值和AB的长;
(2)(图2)若P、Q运动t秒后第一次在C处相遇,再经过
t秒,P从B处返回并在E处追上Q;求VP:VQ;
(3)在(2)的条件下,若t=4,当它们第三次在D处相遇时(图3),求此时D点表示的数.
(1)求a、b的值和AB的长;
(2)(图2)若P、Q运动t秒后第一次在C处相遇,再经过
| 4 |
| 3 |
(3)在(2)的条件下,若t=4,当它们第三次在D处相遇时(图3),求此时D点表示的数.

考点:一元一次方程的应用,数轴,两点间的距离
专题:应用题
分析:(1)根据非负数的性质得到a+7=0,3a+b=0,再解方程得到a=-7;b=21,然后用B点表示的数减去A点表示的数得到AB的长;
(2)P、Q运动t秒后第一次在C处相遇,根据路程不变列方程得t(VP+VQ)=28,再根据P从B处返回并在E处追上Q得到(
t+t)VP=28+(
t+t)VQ,
变形后可得VP:VQ=5:2;
(3)有(2)得4VP+4VQ=28,所以10VQ+4VQ=28,解得VQ=2,VP=5,则计算出AE=AB-VQ•(t+
t)=
,设再经过m秒,P、Q第三次在D点相遇,
点P从E点到A点再到D点,则5m+2m=2×
,解得m=
,得到AD=AE-DE=4,而点A表示的数为-7,所以D点表示的数是-3.
(2)P、Q运动t秒后第一次在C处相遇,根据路程不变列方程得t(VP+VQ)=28,再根据P从B处返回并在E处追上Q得到(
| 4 |
| 3 |
| 4 |
| 3 |
变形后可得VP:VQ=5:2;
(3)有(2)得4VP+4VQ=28,所以10VQ+4VQ=28,解得VQ=2,VP=5,则计算出AE=AB-VQ•(t+
| 4 |
| 3 |
| 28 |
| 3 |
点P从E点到A点再到D点,则5m+2m=2×
| 28 |
| 3 |
| 8 |
| 3 |
解答:解:(1)根据题意得a+7=0,3a+b=0,解得a=-7;b=21,
AB=21-(-7)=28;
(2)根据题意得t(VP+VQ)=28,
(
t+t)VP=28+(
t+t)VQ,
所以(
t+t)VP=t(VP+VQ)+(
t+t)VQ,
解得VP:VQ=5:2;
(3)根据题意得4VP+4VQ=28,
所以10VQ+4VQ=28,解得VQ=2,VP=5,
AE=28-2×(4+
×4)=
,
设再经过m秒,P、Q第三次在D点相遇,
依题意得5m+2m=2×
,解得m=
,
所以AD=AE-DE=
-2×
=4,
而点A表示的数为-7,
所以D点表示的数是-3.
AB=21-(-7)=28;
(2)根据题意得t(VP+VQ)=28,
(
| 4 |
| 3 |
| 4 |
| 3 |
所以(
| 4 |
| 3 |
| 4 |
| 3 |
解得VP:VQ=5:2;
(3)根据题意得4VP+4VQ=28,
所以10VQ+4VQ=28,解得VQ=2,VP=5,
AE=28-2×(4+
| 4 |
| 3 |
| 28 |
| 3 |
设再经过m秒,P、Q第三次在D点相遇,
依题意得5m+2m=2×
| 28 |
| 3 |
| 8 |
| 3 |
所以AD=AE-DE=
| 28 |
| 3 |
| 8 |
| 3 |
而点A表示的数为-7,
所以D点表示的数是-3.
点评:本题考查了一元一次方程的应用:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.也考查了速度公式、数轴和两点间的距离.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,△ABC≌△CDA,AB=5,BC=7,AC=6,则AD边的长为( )
如图,△ABC≌△CDA,AB=5,BC=7,AC=6,则AD边的长为( )| A、5 | B、6 | C、7 | D、不确定 |
2.796精确到百分位的结果是( )
| A、2.79 | B、2.81 |
| C、2.7 | D、2.80 |
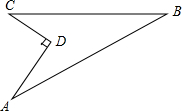 如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?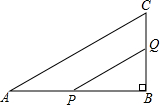 在△ACB中,∠B=90°,AB=6cm,BC=3cm,点P从A点开始沿着AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发:
在△ACB中,∠B=90°,AB=6cm,BC=3cm,点P从A点开始沿着AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发: