题目内容
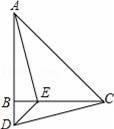
如图，在直角三角形ABC中，∠C=90°，∠CAB的平分线ADD交BC于点D，若DE垂直平分AB，则下列结论中错误的是( )
A．AB=2AE B．AC=2CD C．DB=2CD D．AD=2DE
B【考点】线段垂直平分线的性质；角平分线的性质；含30度角的直角三角形．
【分析】根据线段的垂直平分线的性质，等腰三角形的性质，角平分线的性质求出求出∠CAD=∠BAD=∠B=30°，根据30°角的直角三角形的性质即可判断．
【解答】解：∵DE垂直平分AB，
∴AD=BD，AB=2AE，
∴∠DAB=∠B，
∵∠CAD=∠DAB=
∠BAC，
∴∠BAC=2∠B，
∵∠C=90°，
∴∠B=30°，∠BAC=60°，
∴∠CAD=∠DAB=30°，
∴AD=2CD，BD=AD=2DE，
∵AD是∠CAB的平分线，DC⊥AC，DE⊥AB，
∴DE=CD，
∴BD=2CD，
∵AD=2CD，AD＞AC，
∴AC≠2CD，
故选B．
【点评】本题考查了三角形的内角和定理，线段垂直平分线的性质，角平分线的性质，等腰三角形的判定，含30度角的直角三角形的性质的应用，注意：在直角三角形中，如果有一个角等于30°，那么它所对的直角边等于斜边的一半．
大小关系正确的是（ ）
某校体育组长王老师，到家乐福超市为学校购买乒乓球拍、羽毛球拍共三次，有一次购买时，乒乓球拍、羽毛球拍同时打折，其余两次均按标价购买，三次购买乒乓球拍、羽毛球拍数量及费用如表：
| 乒乓球拍的数量（副） | 羽毛球拍的数量（副） | 总费用（元） | |
| 第一次购买 | 6 | 5 | 1140 |
| 第二次购买 | 3 | 7 | 1110 |
| 第三次购买 | 9 | 8 | 1062 |
（1）按打折价购买乒乓球拍、羽毛球拍是第几次购买？
（2）求乒乓球拍、羽毛球拍的标价；
（3）若乒乓球拍、羽毛球拍的折扣相同，问家乐福超市是打几折出售的？
．
B．
C．
D．