题目内容
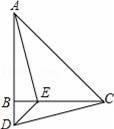
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.

【考点】全等三角形的判定与性质;三角形的外角性质.
【专题】证明题.
【分析】①利用SAS即可得证;
②由全等三角形对应角相等得到∠AEB=∠CDB,利用外角的性质求出∠AEB的度数,即可确定出∠BDC的度数.
【解答】①证明:在△ABE和△CBD中,

 ,
,
∴△ABE≌△CBD(SAS);
②解:∵△ABE≌△CBD,
∴∠AEB=∠BDC,
∵∠AEB为△AEC的外角,
∴∠AEB=∠ACB+∠CAE=30°+45°=75°,
则∠BDC=75°.
【点评】此题考查了全等三角形的判定与性质,以及三角形的外角性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目

 是同类项,则a的值是( )
是同类项,则a的值是( )
 B.﹣2 C.2 D.
B.﹣2 C.2 D.


 =
=
 的解为 .
的解为 .