题目内容
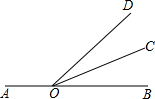 如图,点O在直线AB上,OC平分∠DOB.若∠COB=36°.
如图,点O在直线AB上,OC平分∠DOB.若∠COB=36°.(1)求∠DOB的大小;
(2)请你用量角器先画∠AOD的角平分线OE,再说明OE和OC的位置关系.
考点:角平分线的定义
专题:
分析:(1)根据角平分线定义求出∠BOD;
(2)根据题意画出图形,然后利用角平分线和平角的定义得到∠EOC=90°,所以OE⊥OC.
(2)根据题意画出图形,然后利用角平分线和平角的定义得到∠EOC=90°,所以OE⊥OC.
解答: 解:(1)∵射线OC平分∠DOB,∠COB=36°,
解:(1)∵射线OC平分∠DOB,∠COB=36°,
∴∠BOD=2∠COB=72°,
即:∠DOB=72°;
(2)OE和OC位置关系是互相垂直;理由如下:
∵OE平分∠AOD,
∴∠AOE=∠DOE,
∵∠AOE=∠DOE,∠AOE+∠DOE+∠BOD=180°,
∴∠EOD+∠COD=
∠AOB=90°,即∠EOC=90°,
∴OE⊥OC.
 解:(1)∵射线OC平分∠DOB,∠COB=36°,
解:(1)∵射线OC平分∠DOB,∠COB=36°,∴∠BOD=2∠COB=72°,
即:∠DOB=72°;
(2)OE和OC位置关系是互相垂直;理由如下:
∵OE平分∠AOD,
∴∠AOE=∠DOE,
∵∠AOE=∠DOE,∠AOE+∠DOE+∠BOD=180°,
∴∠EOD+∠COD=
| 1 |
| 2 |
∴OE⊥OC.
点评:本题考查了角平分线定义和角的有关计算的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
△ABC的顶点A的坐标为(-2,4),先将△ABC沿x轴对折,再向左平移两个单位,此时A点的坐标为( )
| A、(2,-4) |
| B、(0,-4) |
| C、(-4,-4) |
| D、(0,4) |
若抛物线y=ax2-2x+3的顶点坐标为(2,-3),则该抛物线有( )
| A、最大值-3 | B、最小值-3 |
| C、最大值2 | D、最小值2 |
下列函数中,y是x的二次函数的是( )
| A、y=3x+1 | ||
| B、xy=8 | ||
C、y=
| ||
| D、y=x2-x+5 |