题目内容
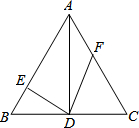 如图,已知△ABC中,AB=AC,D为BC中点,DE⊥AB于E,且DE=3,F是AC上一动点,则DF的最小值为( )
如图,已知△ABC中,AB=AC,D为BC中点,DE⊥AB于E,且DE=3,F是AC上一动点,则DF的最小值为( )| A、3 | B、4 | C、5 | D、不能确定 |
考点:角平分线的性质,垂线段最短
专题:
分析:根据垂线段最短的性质可知,当DF⊥AC于F时DF的值最小.由等腰三角形三线合一的性质得出AD平分∠BAC,再根据角平分线的性质可得此时DF=DE=3.
解答:解:当DF⊥AC于F时DF的值最小.
∵AB=AC,D为BC中点,
∴AD平分∠BAC,
∵DE⊥AB于E,DF⊥AC于F,
∴DF=DE=3.
故选A.
∵AB=AC,D为BC中点,
∴AD平分∠BAC,
∵DE⊥AB于E,DF⊥AC于F,
∴DF=DE=3.
故选A.
点评:本题考查了角平分线的性质,等腰三角形的性质,垂线段最短的应用,注意:角平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目
从下面三个统计图中,可以判断哪个学校的女生人数最多?( )


| A、甲校 | B、乙校 |
| C、丙校 | D、无法确定 |
计算b2•b3正确的结果是( )
| A、2b6 |
| B、2b5 |
| C、b6 |
| D、b5 |
下列各式中,运算正确的是( )
| A、a6÷a3=a2 |
| B、(a3)2=a5 |
| C、(2a)-1=-2a |
| D、a•a2+a3=2a3 |
函数y=
的自变量x的取值范围是( )
| 1 |
| 2x-1 |
A、x<
| ||
B、x>
| ||
C、x=
| ||
D、x≠
|
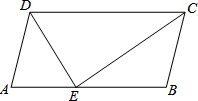 如图,在平行四边形ABCD中,E是AB 上一点,DE、CE分别是∠ADC、∠BCD的平分线.若AD=5,DE=6,则平行四边形ABCD的面积是( )
如图,在平行四边形ABCD中,E是AB 上一点,DE、CE分别是∠ADC、∠BCD的平分线.若AD=5,DE=6,则平行四边形ABCD的面积是( )