题目内容
如果x4-x3+mx2-2mx-2能分解成两个整数系数的二次因式的积,试求m的值,并把这个多项式分解因式.
考点:因式分解的应用
专题:
分析:由于(x2)2-x3+mx2-2mx-2能分解成两个整数系数的二次因式的积,可设(x2)2-x3+mx2-2mx-2=(x2+ax-1)(x2+bx+2)或(x2+ax+1)(x2+bx-2).展开利用对应项的系数相等即可得出.
解答:解:∵(x2)2-x3+mx2-2mx-2能分解成两个整数系数的二次因式的积,
∴可设(x2)2-x3+mx2-2mx-2=(x2+ax-1)(x2+bx+2)或(x2+ax+1)(x2+bx-2).
①(x2+ax-1)(x2+bx+2)=x4+(a+b)x3+(1+ab)x2+(2a-b)x-2,
∴
,
解得m=1或
.
②(x2+ax+1)(x2+bx-2)=x4+(a+b)x3+(ab-1)x2+(b-2a)x-2,
∴
,
解得m=-1或-
.
综上可得:m的值为1或
或-1或-
.
∴可设(x2)2-x3+mx2-2mx-2=(x2+ax-1)(x2+bx+2)或(x2+ax+1)(x2+bx-2).
①(x2+ax-1)(x2+bx+2)=x4+(a+b)x3+(1+ab)x2+(2a-b)x-2,
∴
|
解得m=1或
| 7 |
| 4 |
②(x2+ax+1)(x2+bx-2)=x4+(a+b)x3+(ab-1)x2+(b-2a)x-2,
∴
|
解得m=-1或-
| 7 |
| 4 |
综上可得:m的值为1或
| 7 |
| 4 |
| 7 |
| 4 |
点评:本题考查了因式分解的应用.其中涉及到了多项式的运算性质及其恒等式,考查了计算能力,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
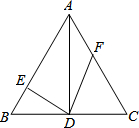 如图,已知△ABC中,AB=AC,D为BC中点,DE⊥AB于E,且DE=3,F是AC上一动点,则DF的最小值为( )
如图,已知△ABC中,AB=AC,D为BC中点,DE⊥AB于E,且DE=3,F是AC上一动点,则DF的最小值为( )| A、3 | B、4 | C、5 | D、不能确定 |
 已知函数y1=x+b1与函数y2=-x+b2的图象如图所示,则不等式y1<y2的解集为( )
已知函数y1=x+b1与函数y2=-x+b2的图象如图所示,则不等式y1<y2的解集为( )| A、x>1 | B、x<1 |
| C、x<0 | D、x<2 |
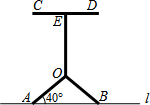 有一种小凳的示意图如图所示,支柱OE与地面l垂直,小凳表面CD与地面l平行,凳腿OA与地面l的夹角为40°,OE=35cm,OA=OB=25cm.求小凳表面CD与地面
有一种小凳的示意图如图所示,支柱OE与地面l垂直,小凳表面CD与地面l平行,凳腿OA与地面l的夹角为40°,OE=35cm,OA=OB=25cm.求小凳表面CD与地面 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…
如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…