题目内容
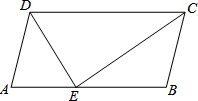 如图,在平行四边形ABCD中,E是AB 上一点,DE、CE分别是∠ADC、∠BCD的平分线.若AD=5,DE=6,则平行四边形ABCD的面积是( )
如图,在平行四边形ABCD中,E是AB 上一点,DE、CE分别是∠ADC、∠BCD的平分线.若AD=5,DE=6,则平行四边形ABCD的面积是( )| A、96 | B、60 | C、48 | D、30 |
考点:平行四边形的性质
专题:
分析:利用平行四边形的性质结合角平分线的性质得出DA=AE=5,BC=BE=5,进而利用勾股定理得出DF的长,即可得出平行四边形ABCD的面积.
解答: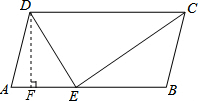 解:过点D作DF⊥AB于点F,
解:过点D作DF⊥AB于点F,
∵DE、CE分别是∠ADC、∠BCD的平分线,
∴∠ADE=∠CDE,∠DCE=∠BCE,
∵四边形ABCD是平行四边形,
∴AB∥DC,AD=BC=5,
∠CDE=∠DEA,∠DCE=∠CEB,
∴∠ADE=∠AED,∠CBE=∠BEC,
∴DA=AE=5,BC=BE=5,
∴AB=10,
则DF2=DE2-EF2=AD2-AF2,
故62-FE2=52-(5-EF)2,
解得:EF=3.6,
则DE=
=4.8,
故平行四边形ABCD的面积是:4.8×10=48.
故选:C.
 解:过点D作DF⊥AB于点F,
解:过点D作DF⊥AB于点F,∵DE、CE分别是∠ADC、∠BCD的平分线,
∴∠ADE=∠CDE,∠DCE=∠BCE,
∵四边形ABCD是平行四边形,
∴AB∥DC,AD=BC=5,
∠CDE=∠DEA,∠DCE=∠CEB,
∴∠ADE=∠AED,∠CBE=∠BEC,
∴DA=AE=5,BC=BE=5,
∴AB=10,
则DF2=DE2-EF2=AD2-AF2,
故62-FE2=52-(5-EF)2,
解得:EF=3.6,
则DE=
| DE2-EF2 |
故平行四边形ABCD的面积是:4.8×10=48.
故选:C.
点评:此题主要考查了平行四边形的性质以及勾股定理等知识,得出EF,DE的长是解题关键.

练习册系列答案
相关题目
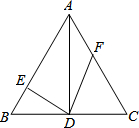 如图,已知△ABC中,AB=AC,D为BC中点,DE⊥AB于E,且DE=3,F是AC上一动点,则DF的最小值为( )
如图,已知△ABC中,AB=AC,D为BC中点,DE⊥AB于E,且DE=3,F是AC上一动点,则DF的最小值为( )| A、3 | B、4 | C、5 | D、不能确定 |
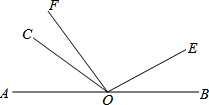 已知点O是直线AB上的一点,∠COE=120°,射线OF是∠AOE的一条三等分线,且∠AOF=
已知点O是直线AB上的一点,∠COE=120°,射线OF是∠AOE的一条三等分线,且∠AOF= 如图,“日”字形窗厨的木条总长是7cm,若窗框的宽是xcm,那么窗框的高是
如图,“日”字形窗厨的木条总长是7cm,若窗框的宽是xcm,那么窗框的高是