题目内容
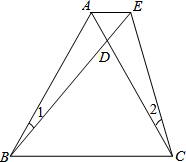 如图,已知△ABC为等边三角形,D为AC上一点,∠1=∠2,BD=CE.求证:△ADE为等边三角形.
如图,已知△ABC为等边三角形,D为AC上一点,∠1=∠2,BD=CE.求证:△ADE为等边三角形.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:由条件可以证明△ABD≌△ACE,进一步得出AD=AE,∠BAC=∠DAE=60°,即可证明△ADE为等边三角形.
解答:证明:∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE=60°
∴△ADE为等边三角形.
∴∠BAC=60°,AB=AC,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE=60°
∴△ADE为等边三角形.
点评:本题考查了等边三角形的判定与性质,难度适中,关键找出判定三角形等边的条件.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
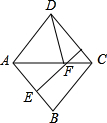 如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )
如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )| A、100° | B、104° |
| C、105° | D、110° |
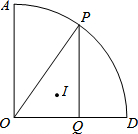 如图,扇形AOD中,∠AOD=90°,OA=6,点P为弧AD上任意一点(不与点A和D重合),PQ⊥OD于Q,点I为△OPQ的内心,过O,I和D三点的圆的半径为r.则当点P
如图,扇形AOD中,∠AOD=90°,OA=6,点P为弧AD上任意一点(不与点A和D重合),PQ⊥OD于Q,点I为△OPQ的内心,过O,I和D三点的圆的半径为r.则当点P在弧AD上运动时,r的值满足( )
| A、0<r<3 | ||
| B、r=3 | ||
C、3<r<3
| ||
D、r=3
|
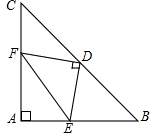 如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.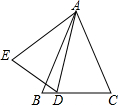 如图,已知在△ABC中,D为BC上的一点,AD平分∠EDC,且∠E=∠B,ED=DC.求证:AB=AC.
如图,已知在△ABC中,D为BC上的一点,AD平分∠EDC,且∠E=∠B,ED=DC.求证:AB=AC.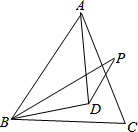 如图,D是等边三角形ABC内一点,DB=DA,BP=AB,∠DPB=∠DBC.求证:∠BPD=30°.
如图,D是等边三角形ABC内一点,DB=DA,BP=AB,∠DPB=∠DBC.求证:∠BPD=30°.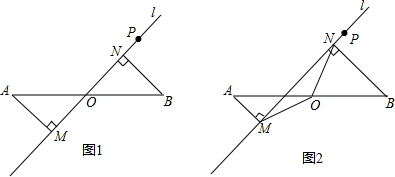
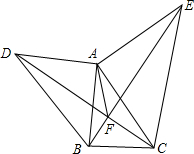 如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连结DC、BE交于F点.
如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连结DC、BE交于F点.