题目内容
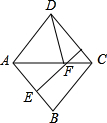 如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )
如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )| A、100° | B、104° |
| C、105° | D、110° |
考点:菱形的性质,线段垂直平分线的性质
专题:
分析:根据菱形的性质求出∠DAB=2∠DAC,AD=CD;再根据垂直平分线的性质得出AF=DF,利用三角形内角和定理可以求得3∠CAD+∠CDF=180°,从而得到∠DAB的度数.
解答: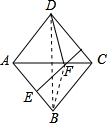 解:连接BD,BF,
解:连接BD,BF,
∵四边形ABCD是菱形,
∴AD=CD,
∴∠DAC=∠DCA.
∵EF垂直平分AB,AC垂直平分BD,
∴AF=BF,BF=DF,
∴AF=DF,
∴∠FAD=∠FDA,
∴∠DAC+∠FAD+∠DCA+∠CDF=180°,即3∠DAC+∠CDF=180°,
∵∠CDF=24°,
∴3∠DAC+24°=180°,则∠DAC=52°,
∴∠DAB=2∠DAC=104°.
故选:B.
 解:连接BD,BF,
解:连接BD,BF,∵四边形ABCD是菱形,
∴AD=CD,
∴∠DAC=∠DCA.
∵EF垂直平分AB,AC垂直平分BD,
∴AF=BF,BF=DF,
∴AF=DF,
∴∠FAD=∠FDA,
∴∠DAC+∠FAD+∠DCA+∠CDF=180°,即3∠DAC+∠CDF=180°,
∵∠CDF=24°,
∴3∠DAC+24°=180°,则∠DAC=52°,
∴∠DAB=2∠DAC=104°.
故选:B.
点评:此题主要考查线段的垂直平分线的性质和菱形的性质,有一定的难度,解答本题时注意先先连接BD,BF,这是解答本题的突破口.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
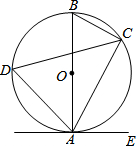 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
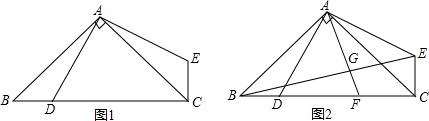
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.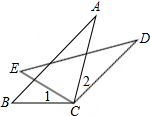 如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由.
如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由.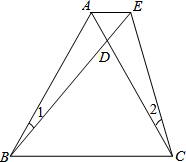 如图,已知△ABC为等边三角形,D为AC上一点,∠1=∠2,BD=CE.求证:△ADE为等边三角形.
如图,已知△ABC为等边三角形,D为AC上一点,∠1=∠2,BD=CE.求证:△ADE为等边三角形.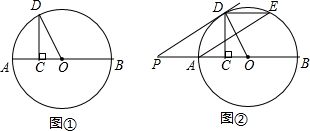
 已知,如图所示,折叠长方形OABC的一边BC,折痕为CE,使点B落在OA边的点D处,如果AB=8,BC=10.求:
已知,如图所示,折叠长方形OABC的一边BC,折痕为CE,使点B落在OA边的点D处,如果AB=8,BC=10.求: