题目内容
已知点O为线段AB的中点,P为线段AB外一点,过P作直线l,分别过A、B作直线l的垂线段AM、BN;
(1)当点O在直线l上时,求证:OM=ON;
(2)直角三角形斜边上的中线有下列性质:斜边上的中线等于斜边的一半.
请你利用这一性质回答问题:当点O不在直线l上时,OM=ON吗?
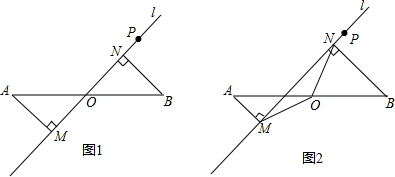
(1)当点O在直线l上时,求证:OM=ON;
(2)直角三角形斜边上的中线有下列性质:斜边上的中线等于斜边的一半.
请你利用这一性质回答问题:当点O不在直线l上时,OM=ON吗?

考点:全等三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:(1)证出△AMO≌△BNO,据此即可解答;
(2)作AC∥l,延长BN交AC于C,连接OC;作BD∥l,延长AM交BD于D,连接OD.证出△MAO≌△NCO即可解答.
(2)作AC∥l,延长BN交AC于C,连接OC;作BD∥l,延长AM交BD于D,连接OD.证出△MAO≌△NCO即可解答.
解答:解:(1)在Rt△AMO和Rt△BNO中,
,
∴△AMO≌△BNO(AAS),
∴OM=ON.
(2)OM=ON.
作AC∥l,延长BN交AC于C,连接OC;作BD∥l,延长AM交BD于D,连接OD.
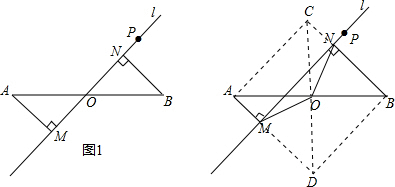 可知,∠ACB=90°,AM=CN.
可知,∠ACB=90°,AM=CN.
∵O为AB的中点,
∴CO=AO,
∴∠OAC=∠OCA,
∴∠OAM=∠OCN,
在△MAO和△NCO中,
,
∴△MAO≌△NCO(ASA),
∴OM=ON.
|
∴△AMO≌△BNO(AAS),
∴OM=ON.
(2)OM=ON.
作AC∥l,延长BN交AC于C,连接OC;作BD∥l,延长AM交BD于D,连接OD.
 可知,∠ACB=90°,AM=CN.
可知,∠ACB=90°,AM=CN.∵O为AB的中点,
∴CO=AO,
∴∠OAC=∠OCA,
∴∠OAM=∠OCN,
在△MAO和△NCO中,
|
∴△MAO≌△NCO(ASA),
∴OM=ON.
点评:本题考查了全等三角形的性质,直角三角形斜边上的中线,正确作出辅助线,构造所需图形是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
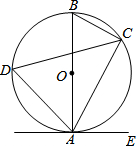 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.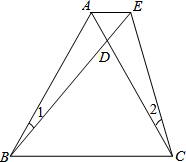 如图,已知△ABC为等边三角形,D为AC上一点,∠1=∠2,BD=CE.求证:△ADE为等边三角形.
如图,已知△ABC为等边三角形,D为AC上一点,∠1=∠2,BD=CE.求证:△ADE为等边三角形.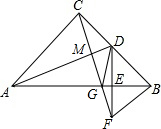 如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连CF,交AB于点G、交AD于点M,连DG.
如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连CF,交AB于点G、交AD于点M,连DG.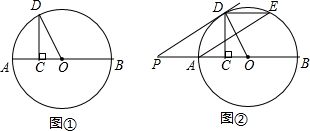
 如图,已知边长为a的正方形ABCD内有一边长为b的内接正方形EFGH,则△EBF的内切圆半径是
如图,已知边长为a的正方形ABCD内有一边长为b的内接正方形EFGH,则△EBF的内切圆半径是 如图,在平面直角坐标系中,直线l是一次函数,点M(2,5)的关于直线l的对称点为M′,求点M′的坐标.
如图,在平面直角坐标系中,直线l是一次函数,点M(2,5)的关于直线l的对称点为M′,求点M′的坐标. 如图,O是矩形ABCD对角线的交点,DE∥AC,CE∥BD.
如图,O是矩形ABCD对角线的交点,DE∥AC,CE∥BD.