题目内容
如图所示，已知∠A=27°，∠CBE=90°，∠C=30°，求∠D的度数．考点：三角形的外角性质,三角形内角和定理
专题：
分析：首先根据三角形内角和定理得出∠CEB的度数，再利用三角形外角的性质得出∠D的度数．
解答：解：∵∠CBE=90°，∠C=30°，
∴∠CEB=180°-90°-30°=60°，
∵∠A+∠D=∠CEB，
∴∠D=∠CEB-∠A=60°-27°=33°．
∴∠CEB=180°-90°-30°=60°，
∵∠A+∠D=∠CEB，
∴∠D=∠CEB-∠A=60°-27°=33°．
点评：此题主要考查了三角形内角和定理以及三角形外角的性质，得出∠CEB的度数是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
下面的图形中，中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
如图，在直角坐标平面中，O为原点，点A的坐标为（20，0），点B在第一象限内，BO=10，sin∠BOA=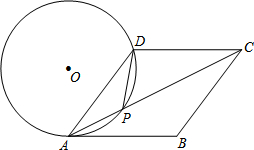
如图，在菱形ABCD中，P是对角线AC上的一点，且PA=PD，⊙O为△APD的外接圆．
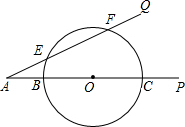已知：如图，∠PAQ=30°，在边AP上顺次截取AB=3cm，BC=10cm，以BC为直径作⊙O交射线AQ于E、F两点，求：