题目内容
如图，四边形ABCD是平行四边形，点E、A、C、F在同一直线上，且AE=CF．求证：BE=DF．考点：平行四边形的性质,全等三角形的判定与性质
专题：证明题
分析：由四边形ABCD是平行四边形，且AE=CF，易证得△BCE≌△DAF，继而证得结论．
解答：证明：∵四边形ABCD为平行四边形，
∴BC=AD，BC∥AD，
∴∠BCA=∠DAC，
又∵AE=CF，
∴EC=AF，
在△BCE和△DAF中，
∴△BCE≌△DAF（SAS），
∴BE=DF．
∴BC=AD，BC∥AD，
∴∠BCA=∠DAC，
又∵AE=CF，
∴EC=AF，
在△BCE和△DAF中，
|
∴△BCE≌△DAF（SAS），
∴BE=DF．
点评：此题考查了平行四边形的性质以．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
2013年宁波市江北区固定资产投资（不含农户投资）完成203.2亿元，同比增长20.9%．其中203.2亿元用科学记数法表示为（ ）
| A、203.2×108元 |
| B、2.032×108元 |
| C、2.032×1010元 |
| D、0.2032×1010元 |
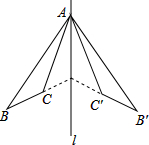如图，△ABC和△A′B′C′关于直线对称，下列结论中：
某学习小组想了解南京市“迎青奥”健身活动的开展情况，准备采用以下调查方式中的一种进行调查：①从一个社区随机选取200名居民；②从一个城镇的不同住宅楼中随机选取200名居民；③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象．
如图，在直角坐标平面中，O为原点，点A的坐标为（20，0），点B在第一象限内，BO=10，sin∠BOA=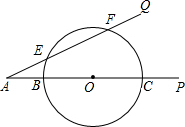
已知：如图，∠PAQ=30°，在边AP上顺次截取AB=3cm，BC=10cm，以BC为直径作⊙O交射线AQ于E、F两点，求：
某商店决定购进一批某种衣服．若商店以每件60元卖出，盈利率为20%（盈利率=