题目内容
16. ①已知△ABC的周长为42,AB=14,边AB上的高为12,则它的内切圆的半径为4
①已知△ABC的周长为42,AB=14,边AB上的高为12,则它的内切圆的半径为4②已知△ABC的三边长分别为5,12,13.则它的内切圆的半径为1
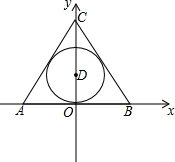
③已知如图.△.ABC中.A、B、C三点的坐标分别为A(-3,0)、B(3,0)、C(0,4).若△ABC内心为D.则点D坐标为(0,$\frac{3}{2}$).
分析 ①利用圆的内切圆的性质以及三角形的面积公式:三角形的面积=$\frac{1}{2}$×三角形的周长×内切圆的半径即可求解.
②先证得△ABC是直角三角形.然后根据三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r计算即可.
③首先根据三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r求得内切圆的半径,即可确定D的坐标,
解答 解:①设内切圆的半径是r,则$\frac{1}{2}$×42r=$\frac{1}{2}$×14×12,
解得:r=4,
即它的内切圆的半径为4.
②∵△ABC的三边长分别为5,12,13.
∴52+122=132,
∴△ABC是直角三角形,
由△ABC的面积=$\frac{1}{2}$×(AB+BC+AC)×r可知:$\frac{1}{2}$(5+12+13)r=$\frac{1}{2}$×5×12.
解得:r=1.
③∵A(-3,O),B(3,O),C(0,4)
∴AB=6,OC=4,
∴AC=BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴$\frac{1}{2}$(6+5+5)r=$\frac{1}{2}$×6×4,
解得:r=$\frac{3}{2}$,
∴D(0,$\frac{3}{2}$).
故答案为:4;1;(0,$\frac{3}{2}$).
点评 本题主要考查了三角形的内切圆和内心,明确三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r是解题的关键.

练习册系列答案
相关题目
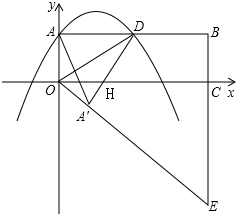 如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,且长分别为1、4,D为边AB的中点,一抛物线l经过点A、D及点M(-1,m).
如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,且长分别为1、4,D为边AB的中点,一抛物线l经过点A、D及点M(-1,m).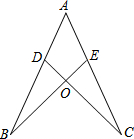 如图,已知:AB=AC,AE=AD,求证:OB=OC.
如图,已知:AB=AC,AE=AD,求证:OB=OC.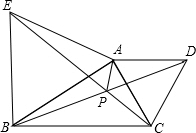 如图,△AEB,△ADC都是等边三角形,BD,CE相交于点P,连接AP.
如图,△AEB,△ADC都是等边三角形,BD,CE相交于点P,连接AP.