题目内容
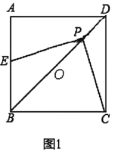
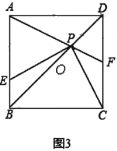
【题目】如图,![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 的平行线与
的平行线与![]() 的平分线交于点
的平分线交于点![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
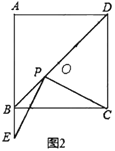
(2)连接![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 的延长线交于
的延长线交于![]() 点,连接
点,连接![]() ,若
,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长为 .
的长为 .
【答案】(1)见解析;(2)2
【解析】
(1)由角平分线的定义和平行线的性质可得∠ABD=∠ADB,可得AB=AD=BC,由菱形的判定可证四边形ABCD是菱形;
(2)由菱形的性质及勾股定理可求OD=OB=2,由直角三角形的性质可求OE的长.
(1)证明:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠ADB
∴AB=AD,
又∵AB=BC,
∴AD=BC,
又∵AD∥BC,
∴四边形ABCD是平行四边形,
又∵AB=BC,
∴平行四边形ABCD是菱形,
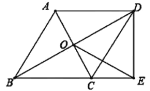
(2)解:∵四边形ABCD是菱形,AC=2,
∴AC⊥BD,OA=OC=![]() AC=1,OB=OD=
AC=1,OB=OD=![]() BD,
BD,
即点O为BD的中点,
又∵![]() ,
,
∴在Rt△BOC中,![]() ,
,
∴BD=2OB=4,
∵DE⊥BC,
∴∠BED=90°,
又∵点O为BD的中点,
∴OE=![]() BD=2.
BD=2.

练习册系列答案
相关题目
【题目】某书店同时购进九年级数学,语文两种辅导书共![]() 册,其进价和售价如下表所示:
册,其进价和售价如下表所示:
数学 | 语文 | |
进价(元/册) |
|
|
售价(元/册) |
|
|
设购进语文辅导书![]() 册.
册.
![]() 已知当该书店购进数学辅导书的数量是语文辅导书的
已知当该书店购进数学辅导书的数量是语文辅导书的![]() 倍时,恰好用去
倍时,恰好用去![]() 元,求
元,求![]() 的值.
的值.
![]() 若设该书店售完这
若设该书店售完这![]() 册辅导书的总利润为
册辅导书的总利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②该书店计划最多投入![]() 元用于购买这两种辅导书,则至少要购进多少册语文辅导书?书店可获得的最大利润是多少?
元用于购买这两种辅导书,则至少要购进多少册语文辅导书?书店可获得的最大利润是多少?