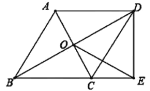
题目内容
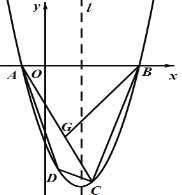
【题目】已知,如图,二次函数![]() 图像交
图像交![]() 轴于
轴于![]() ,交
,交![]() 交轴于点
交轴于点![]() ,
,![]() 是抛物线的顶点,对称轴
是抛物线的顶点,对称轴![]() 经过
经过![]() 轴上的点
轴上的点![]() .
.
(1)求二次函数关系式;
(2)对称轴![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为对称轴
为对称轴![]() 上一动点.
上一动点.
①求![]() 的最小值及取得最小值时点
的最小值及取得最小值时点![]() 的坐标;
的坐标;
②在①的条件下,把![]() 沿着
沿着![]() 轴向右平移
轴向右平移![]() 个单位长度
个单位长度![]() 时,设
时,设![]() 与
与![]() 重叠部分面积记为
重叠部分面积记为![]() ,求
,求![]() 与
与![]() 之间的函数表达式,并求出
之间的函数表达式,并求出![]() 的最大值.
的最大值.
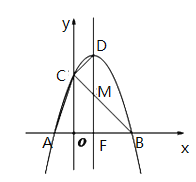
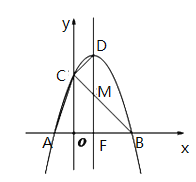
【答案】(1)![]() ;(2)①最小值为
;(2)①最小值为![]() ,点
,点![]() 坐标为
坐标为![]() ;②
;②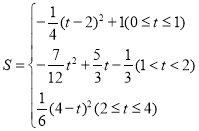 ,当
,当![]() 时,
时,![]() 最大值
最大值![]() .
.
【解析】
(1)函数对称轴为x=1,则点B(3,0),用交点式表达式得:y=a(x+1)(x-3)=a(x2-2x-3),即可求解;
(2)①连接BD,过点A作AH⊥BD于点H,交DF于点P,AP+![]() PD=AP+PD,此时AP+
PD=AP+PD,此时AP+![]() PD=AH最小,即可求解;
PD=AH最小,即可求解;
②根据题意,可分为0≤t≤1、1<t<2、2≤t≤4三种情况,分别求解,即可得到答案.
解:(1)二次函数![]() 对称轴为
对称轴为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,
则点![]() 坐标为
坐标为![]() .
.
又∵点![]() 坐标
坐标![]() ,则
,则
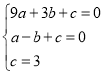 ,解得:
,解得: ,
,
∴函数表达式为![]() ;
;
(2)①连接![]()
∵![]()
∴![]()
在![]() 中,依勾股定理得:
中,依勾股定理得:![]()
∴![]()
过点![]() 作
作![]() 于点
于点![]() ,交抛物线对称轴于点
,交抛物线对称轴于点![]()
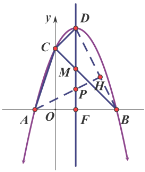
则![]()
则![]()
依“垂线段最短”得此时![]() 长度为最小值,
长度为最小值,
即![]() 最小值为
最小值为![]() 的长度,
的长度,
∵![]()
则![]() ,
,![]()
即![]() 最小值为
最小值为![]() .
.
点![]() 坐标为
坐标为![]() .
.
②A.当![]() 时,如图
时,如图
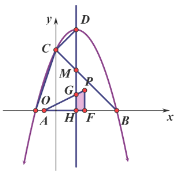
依图知:![]()
则:![]()
![]()
化简得:![]()
配方得:![]()
根据自变量取值范围,当![]() 时,
时,![]() 最大值
最大值![]() 4
4
B.当![]() 时,如图:
时,如图:

![]() 四边形
四边形![]()
![]()
整理得:![]()
配方得:![]()
即![]() 时,
时,![]() 最大值
最大值![]()
C.当![]() 时,如图:
时,如图:
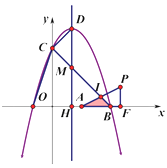
![]()
根据自变量取值范围,当![]() 时,
时,![]() 最大值
最大值![]()
综上,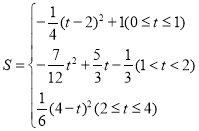 ,当
,当![]() 时,
时,![]() 最大值
最大值![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目