题目内容
(9分)如图,已知数轴上有A、B、C三点,分别表示有理数-26、-10、10,动点P从点A出发,以每秒1个单位的速度向终点C移动,当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,问当点Q从A点出发几秒钟时,点P和点Q相距2个单位长度? 直接写出此时点Q在数轴上表示的有理数.
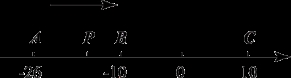
7秒或9秒;-5和1.
【解析】
试题分析:本题需要分两种情况进行讨论,①点Q追上点P之前,点P运动的路程-点Q运动的路程=2;②点Q追上点P之后,点Q运动的路程-点P匀速的路程=2.
试题解析:有两种情况:
(1)点Q追上点P之前相距2个单位长度.
设此时点Q从A点出发t秒钟.依题意,得 (16+t)-3t 解得,t=7.
此时点Q在数轴上表示的有理数为-5.
(2)点Q追上点P之后相距2个单位长度.
设此时点Q从A点出发m秒钟.依题意,得3m-(16+m)=2
解得,m =9.此时点Q在数轴上表示的有理数为1.
综上所述,当点Q从A点出发7秒和9秒时,点P和点Q相距2个单位长度,此时点Q在数轴上表示的有理数分别为-5和1.
考点:动点问题.
考点分析: 考点1:一元一次方程 定义:在一个方程中,只含有一个未知数,并且未知数的指数是1,这样的整式方程叫一元一次方程。注:主要用于判断一个等式是不是一元一次方程。 一元一次方程标准形式:
只含有一个未知数(即“元”),并且未知数的最高次数为1(即“次”)的整式方程叫做一元一次方程。
一元一次方程的标准形式(即所有一元一次方程经整理都能得到的形式)是ax+b=0(a,b为常数,x为未知数,且a≠0)。其中a是未知数的系数,b是常数,x是未知数。未知数一般设为x,y,z。
分类:
1、总量等于各分量之和。将未知数放在等号左边,常数放在右边。如:x+2x+3x=6
2、等式两边都含未知数。如:302x+400=400x,40x+20=60x.
方程特点:
(1)该方程为整式方程。
(2)该方程有且只含有一个未知数。
(3)该方程中未知数的最高次数是1。 一元一次方程判断方法:
通过化简,只含有一个未知数,且含有未知数的最高次项的次数是一的等式,叫 一元一次方程。
要判断一个方程是否为一元一次方程,先看它是否为整式方程。若是,再对它进行整理。如果能整理为 ax+b=0(a≠0)的形式,则这个方程就为一元一次方程。里面要有等号,且分母里不含未知数。
一元一次方程必须同时满足4个条件:
⑴它是等式;
⑵分母中不含有未知数;
⑶未知数最高次项为1;
⑷含未知数的项的系数不为0。
学习实践:
在小学会学习较浅的一元一次方程,到了初中开始深入的了解一元一次方程的解法和利用一元一次方程解较难的应用题。一元一次方程牵涉到许多的实际问题,例如工程问题、植树问题、比赛比分问题、行程问题、行船问题、相向问题分段收费问题、盈亏、利润问题。
列方程时,要先设字母表示未知数,然后根据问题中的相等关系,写出含有未知数的等式—— 方程。
⒈4x=24
⒉1700+150x=2450
⒊0.52x-(1-0.52)x=80
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法. 考点2:有理数 1、有理数的概念:正数和分数统称为有理数.
2、有理数的分类:
①按整数、分数的关系分类; ②按正数、负数与0的关系分类.
有理数{整数{正整数0负整数分数{正分数负分数 有理数 {正数{正整数正分数0负数{负整数负分数
注意:如果一个数是小数,它是否属于有理数,就看它是否能化成分数的形式,所有的有限小数和无限循环小数都可以化成分数的形式,因而属于有理数,而无限不循环小数,不能化成分数形式,因而不属于有理数. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
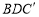 是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 对。
是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 对。

 -1)(
-1)( 2) C.(
2) C.( 1,2) D.(2,1)
1,2) D.(2,1) …,记第一个数
…,记第一个数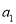 ,第二个数为
,第二个数为 ,…,第n个数为
,…,第n个数为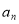 ,若
,若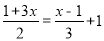 的解,则n =___________.
的解,则n =___________.
 且
且 时,因为
时,因为 ≥
≥ ,所以
,所以 ≥
≥ ≥
≥ (当
(当 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当
,由上述结论可知:当 .
. 与函数
与函数 , 则当
, 则当 _________时,
_________时, 取得最小值为_________.变形应用:
取得最小值为_________.变形应用: 与函数
与函数 ,求
,求 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的 的值.
的值. 元;二是燃油费,每千米为
元;二是燃油费,每千米为 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为 千米,求当
千米,求当