题目内容
(本题满分12分)
知识迁移:
当 且
且 时,因为
时,因为 ≥
≥ ,所以
,所以 ≥
≥ ,从而
,从而 ≥
≥ (当
(当 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为 .
.
直接应用:
已知函数 与函数
与函数 , 则当
, 则当 _________时,
_________时, 取得最小值为_________.变形应用:
取得最小值为_________.变形应用:
已知函数 与函数
与函数 ,求
,求 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的 的值.
的值.
实际应用:
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共 元;二是燃油费,每千米为
元;二是燃油费,每千米为 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为 千米,求当
千米,求当 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
直接应用:1, 2 ;变形应用:当x=1时, 有最小值为4;实际应用:当x为600千米时,该汽车平均每千米的运输成本最低,最低是2.8元.
有最小值为4;实际应用:当x为600千米时,该汽车平均每千米的运输成本最低,最低是2.8元.
【解析】
试题分析:直接运用:可以直接套用套用所给的结论,即可得出结果.
变形运用:先得出 的表达式,然后将(x+1)看作一个整体,继而再运用所给结论即可.
的表达式,然后将(x+1)看作一个整体,继而再运用所给结论即可.
实际运用:设行驶x千米的费用为y,则可表示出平均每千米的运输成本,利用所给的距离即可得出答案.
试题解析:解:直接应用:因为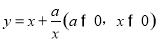 ,由上述结论可知:当x=
,由上述结论可知:当x= 时,该函数有最小值2
时,该函数有最小值2 ,所以函数
,所以函数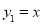
 与函数
与函数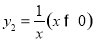 ,则当x=1时,
,则当x=1时,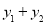 取得最小值为2.
取得最小值为2.
故答案为:1, 2 ;
变形应用:
解:∵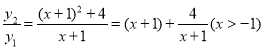 ,
,
∴ 有最小值为
有最小值为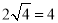 ,
,
当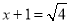 ,即
,即 时取得该最小值.
时取得该最小值.
实际应用:
解:设该汽车平均每千米的运输成本为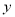 元,则
元,则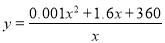
 ,
,
∴当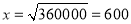 (千米)时, 该汽车平均每千米的运输成本
(千米)时, 该汽车平均每千米的运输成本 最低,最低成本为
最低,最低成本为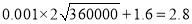 元.
元.
考点:二次函数的应用.
考点分析: 考点1:二次函数 定义:一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案(本题满分10分)某校学生参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如表所示:
销售单价x(单位:元/个) | 10 | 12 | 14 | 16 |
销售量y(单位:个) | 300 | 240 | 180 | 120 |
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;
(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.

 的顶点坐标为_________。
的顶点坐标为_________。 的一元二次方程的两个根为
的一元二次方程的两个根为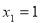 ,
,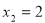 ,则这个方程是( )
,则这个方程是( )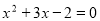 B.
B.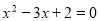
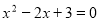 D.
D.