题目内容
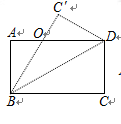
如图所示,△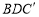 是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 对。
是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 对。
4
【解析】
试题分析:共有四对,分别是△ABD≌△CDB,△ABD≌△C′DB,△DCB≌△C′DB,△AOB≌△C′OD.
分析:∵四边形ABCD是长方形,
∴∠A=∠C=90°,AB=CD,AD=BC,
∴△ABD≌△CDB.(HL)
∵△BDC是将长方形纸牌ABCD沿着BD折叠得到的,
∴BC′=AD,BD=BD,∠C′=∠A.
∴△ABD≌△C′DB.(HL)
同理△DCB≌△C′DB.
∵∠A=∠C′,∠AOB=∠C′OD,AB=C′D,
∴△AOB≌△C′OD.(AAS)
所以共有四对全等三角形.
考点:三角形全等的判定与性质
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
(3)三角形的主要线段:角平分线、中线、高.
(4)三角形具有稳定性. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调、冰箱、彩电共360台,且彩电至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:
| 家电名称 | 空调 | 冰箱 | 彩电 |
| 工时 |
|
|
|
| 产值(千元) | 4 | 3 | 2 |
问每周应生产空调、冰箱、彩电各多少台,才能使产值最高?最高产值是多少?
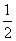
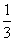
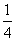


 .
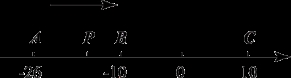
.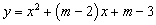 总过x轴上的
总过x轴上的 同侧、
同侧、 异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路
异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路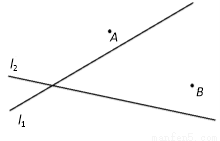
 分解因式,结果正确的是( )
分解因式,结果正确的是( ) C、x(x+y)2 D、x(x+y)(
C、x(x+y)2 D、x(x+y)( )
) 与
与 的和仍是单项式,则
的和仍是单项式,则 的值为____________.
的值为____________.