题目内容
解分式方程:
无解.
【解析】
试题分析:首先进行去分母,将分式方程转化为整式方程,然后按照整式方程的求解方法进行求解,最后对所求的解进行检验,看是否能使分母为零.
试题解析:两边同乘以(x+2)(x-2)得:x(x+2)-(x+2)(x-2)=8
去括号,得: +2x-
+2x- +4=8 移项、合并同类项得:2x=4 解得:x=2
+4=8 移项、合并同类项得:2x=4 解得:x=2
经检验,x=2是方程的增根 ∴方程无解
考点:解分式方程.
考点分析: 考点1:分式 分式:中考试题中分值约为6-8分,主要以填空,简答计算题型出现,难易度属于中。近几年主要考察①分式的概念,性质,意义②分式的运算,化简求值。③列分式方程解决实际问题、突破方法:①掌握并灵活应用分式的基本性质,②在通分和约分时,都要注意分解因式知识的应用。③化简求值时,注意整体思想和技巧的应用。④留意生活中是实际问题 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
(本题满分10分)某校学生参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如表所示:
销售单价x(单位:元/个) | 10 | 12 | 14 | 16 |
销售量y(单位:个) | 300 | 240 | 180 | 120 |
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;
(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
 与
与 的和仍是单项式,则
的和仍是单项式,则 的值为____________.
的值为____________.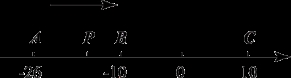
 m)的解满足
m)的解满足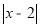 -3=0,则m的值为( )
-3=0,则m的值为( )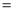 2BD
2BD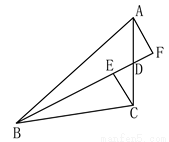
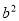 +3,则m和n的大小关系中正确的是( )
+3,则m和n的大小关系中正确的是( )
 的顶点坐标为_________。
的顶点坐标为_________。