题目内容
8.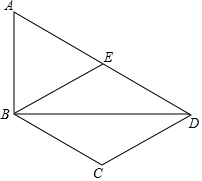 如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
分析 (1)由DE=BC,DE∥BC,推出四边形BCDE是平行四边形,再证明BE=DE即可解决问题;
(2)在Rt△ACD中只要证明∠ADC=60°,AD=2即可解决问题;
解答 (1)证明:∵AD=2BC,E为AD的中点,
∴DE=BC,
∵AD∥BC,
∴四边形BCDE是平行四边形,
∵∠ABD=90°,AE=DE,
∴BE=DE,
∴四边形BCDE是菱形.
(2)解:连接AC.
∵AD∥BC,AC平分∠BAD,
∴∠BAC=∠DAC=∠BCA,
∴AB=BC=1,
∵AD=2BC=2,
∴sin∠ADB=$\frac{1}{2}$,
∴∠ADB=30°,
∴∠DAC=30°,∠ADC=60°,
在Rt△ACD中,∵AD=2,
∴CD=1,AC=$\sqrt{3}$.
点评 本题考查菱形的判定和性质、直角三角形斜边中线的性质、锐角三角函数等知识,解题的关键是熟练掌握菱形的判定方法,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图是某个几何体的展开图,该几何体是( )
如图是某个几何体的展开图,该几何体是( )
 如图是某个几何体的展开图,该几何体是( )
如图是某个几何体的展开图,该几何体是( )| A. | 三棱柱 | B. | 圆锥 | C. | 四棱柱 | D. | 圆柱 |
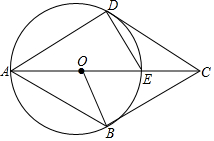 已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D.B点在⊙O上,连接OB.
已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D.B点在⊙O上,连接OB.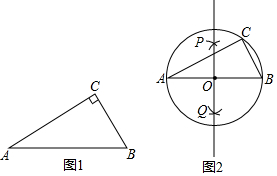 下面是“作已知直角三角形的外接圆”的尺规作图过程
下面是“作已知直角三角形的外接圆”的尺规作图过程