已知AD∥BC.∠A=∠C.问AB∥CD吗?为什么? 题目和参考答案——青夏教育精英家教网—

题目内容

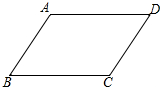已知AD∥BC，∠A=∠C，问AB∥CD吗？为什么？

考点：平行线的判定与性质

专题：常规题型

分析：由AD∥BC，根据两直线平行，同旁内角互补得到∠A+∠B=180°，而∠A=∠C，所以∠C+∠B=180°，然后根据同旁内角互补，两直线平行即可得到AB∥CD．

解答：解：AB∥CD．理由如下：
∵AD∥BC，
∴∠A+∠B=180°，
∵∠A=∠C，
∴∠C+∠B=180°，
∴AB∥CD．

点评：本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．

练习册系列答案

相关题目

如图，在△ABC中，点P是△ABC的外角∠DBC、∠BCE的平分线的交点，若∠BPC=70°，则∠BAC=

度．

钟表的轴心到分针针端的长为4cm，那么经过20分钟，分针针端转过的弧长是

cm（用π表示）．

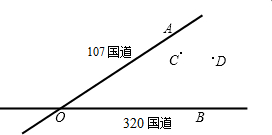作图题，不写作方法但要保留作图痕迹
如图：107国道OA和320 国道OB相交于点O，在∠AOB的内部有工厂C和D．现要修建一个货站P，使P到OA、OB的距离相等，且PC=PD．用尺规作出货站P的位置．

某同学遇到这样一个问题：已知在△ABC中，AB，BC，AC三边的长分别为

、

，求△ABC的面积．他是这样解决问题的：如图1，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处）．从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．请回答：
（1）图1中△ABC的面积为

；
（2）图2是一个6×6的正方形网格（每个小正方形的边长为1）．利用构图法在图2中画出三边长分别为

、2

、

的格点△DEF；
（3）如图3，已知△PQR，以PQ、PR为边向外作正方形PQAF、PRDE，连EF．若PQ=2

．

在解关于x的方程（2x-1）²+3（2x-1）+2=0时，若设y=（2x-1），则方程可以转化为关于y的方程：

试题分类