题目内容
用适当的方法解方程组:
(1)
;
(2)
.
(1)
|
(2)
|
考点:解二元一次方程组
专题:计算题
分析:(1)方程组整理后,利用加减消元法求出解即可;
(2)两方程相加,变形求出x+y的值,利用代入消元法求出解即可.
(2)两方程相加,变形求出x+y的值,利用代入消元法求出解即可.
解答:解:(1)方程组整理得:
,
②×2-①得:y=-7,
把y=-7代入①得:x=7,
则方程组的解为
;
(2)
,
①+②得:40(x+y)=120,即y=3-x,
代入①得:23x+51-17x=63,
解得:x=2,
把x=2代入得:y=1,
则方程组的解为
.
|
②×2-①得:y=-7,
把y=-7代入①得:x=7,
则方程组的解为
|
(2)
|
①+②得:40(x+y)=120,即y=3-x,
代入①得:23x+51-17x=63,
解得:x=2,
把x=2代入得:y=1,
则方程组的解为
|
点评:此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
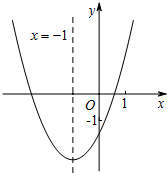 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=-1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=-1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:其中,正确的结论有( )
①abc>0;②-3<x2<-2;③4a+1>2b-c;④4ac-b2+4a<0;⑤a>
| 1 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知二次函数y=2x2+x+m的图象与x轴有唯一交点,则当-1≤x≤0时,y的取值范围是( )
A、0≤y≤
| ||
B、-
| ||
C、0<y<
| ||
D、-
|
轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同.已知水流的速度是3千米/时,求轮船在静水中的速度.设轮船在静水中的速度为x千米/时,由题意列出方程,其中正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=
的自变量取值范围为( )
| ||
| 2 |
| A、x≤1 | B、x≤-1 |
| C、x>1 | D、x≥-1 |
 如图,在△ABC中,∠BAC=40°,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数为
如图,在△ABC中,∠BAC=40°,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数为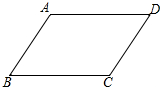 已知AD∥BC,∠A=∠C,问AB∥CD吗?为什么?
已知AD∥BC,∠A=∠C,问AB∥CD吗?为什么? 已知∠3+∠2=180°,∠1=45°,求∠4的度数.
已知∠3+∠2=180°,∠1=45°,求∠4的度数.