Question

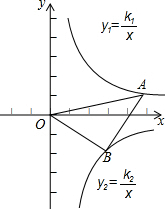如图，在平面直角坐标系中，反比例函数y₁=

k1

x

（x＞0）的图象与反比y₂=

k2

x

（x＞0）的图象关于x轴对称，若有一个等腰Rt△OAB，∠OBA=90°，点A在图象y₁上，点B在图象y₂上，若点B的纵坐标为-2，则点A的纵坐标为

 

．

Answer 1

考点：反比例函数综合题

专题：

分析：根据反比例函数y₁=

k1

x

（x＞0）的图象与反比y₂=

k2

x

（x＞0）的图象关于x轴对称，可得k₂=-k₁，设点A纵坐标为m，分别表示出点A、B的坐标，然后根据△OAB为等腰直角三角形，可得OB=AB，OB²+AB²=OA²，列方程求解即可．

解答：解：∵y₁与y₂的图象关于x轴对称，
∴k₂=-k₁，
设点A纵坐标为m，
则点A横坐标为：

k1

m

，OA=

m2+ k 2 1 m2

，
∵点B的纵坐标为-2，
∴点B横坐标为：

k1

2

，
OB=

k 2 1 4 +4

，AB=

( k1 m - k1 2 )2+(m+2)2

，
∵△OAB为等腰直角三角形，
∴OB=AB，OB²+AB²=OA²，
即

k 2 1 4 +4

=

( k1 m - k1 2 )2+(m+2)2

，

k 2 1

4

+4+（

k1

m

-

k1

2

）²+（m+2）²=m²+

k 2 1

m2

，
解得：k₁²=8（3+

5

），m=

5

-1．
即点A的纵坐标为

5

-1．
故答案为：

5

-1．

点评：本题考查了反比例函数的综合应用，解答本题的关键是能够判定k₂=-k₁，得出点A和点B的坐标，运用勾股定理以及等腰直角三角形的性质将AB、OA、OB的长度代入列方程求解．