题目内容
把方程(x-2)2=4x+(2x-1)2化成一元二次方程的一般形式,得 .
考点:二次函数的三种形式
专题:
分析:一元二次方程的一般式:ax2+bx+c=0(a≠0,a,b,c为常数).先去括号,再移项,最后合并即可.
解答:解:移项,得
(x-2)2-(2x-1)2-4x=0,
去括号,得
x2-4x+4-4x2+4x-1-4x=0,
合并同类项,得
-3x2-4x+3=0,
或3x2+4x-3=0.
故答案是:3x2+4x-3=0.
(x-2)2-(2x-1)2-4x=0,
去括号,得
x2-4x+4-4x2+4x-1-4x=0,
合并同类项,得
-3x2-4x+3=0,
或3x2+4x-3=0.
故答案是:3x2+4x-3=0.
点评:本题考查的是一元二次方程的一般形式,通过去括号,移项,合并同类项,可以把方程化为一般形式.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
下列计算正确的是( )
| A、(-1)0=-1 | ||
| B、(-1)-1=1 | ||
C、2a-3=
| ||
D、(-a5)÷(-a)7=
|
若把分式
中x、y都扩大3倍,那么分式的值( )
| 5xy |
| x+y |
| A、扩大3倍 | B、不变 |
| C、缩小3倍 | D、缩小6倍 |
方程x2+3x-1=0的两个根的符号为( )
| A、同号 | B、异号 |
| C、两根都为正 | D、不能确定 |
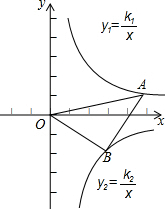 如图,在平面直角坐标系中,反比例函数y1=
如图,在平面直角坐标系中,反比例函数y1=