题目内容
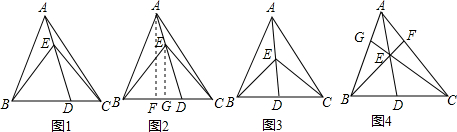
问题引入:如图,在△ABC中,D是BC上一点,AE=
AD,求
:
尝试探究:过点A作BC的垂线,垂足为F,过点E作BC的垂线,垂足为G,如图所示,有
= ,
= ,
.
类比延伸:若E为AD上的任一点,如图所示,试猜S四边形ABEC与S△ABC的比是图中哪条线段的比,并加以证明.
拓展应用:如图,E为△ABC内一点,射线AE于BC于点D,射线BE交AC于点F,射线CE交AB于点G,求
+
+
的值.
| 1 |
| 3 |
| S四边形ABEC |
| S△ABC |
尝试探究:过点A作BC的垂线,垂足为F,过点E作BC的垂线,垂足为G,如图所示,有
| EG |
| AF |
| S△BCE |
| S△ABC |
| S四边形ABEC |
| S△ABC |
类比延伸:若E为AD上的任一点,如图所示,试猜S四边形ABEC与S△ABC的比是图中哪条线段的比,并加以证明.
拓展应用:如图,E为△ABC内一点,射线AE于BC于点D,射线BE交AC于点F,射线CE交AB于点G,求
| AE |
| AD |
| BE |
| BF |
| CE |
| CG |

考点:面积及等积变换
专题:
分析:问题引入:由D是BC上一点,AE=
AD,根据等高三角形的面积比等于对应底的比,可得:
=
,
=
,继而求得答案;
尝试探究:由AF⊥BC,EG⊥BC,易证得△EDG∽△ADB,然后由相似三角形的性质,求得
的值,再利用等底三角形的面积比等于对应高的比,即可求得
的值,继而求得
的值;
类比延伸:由E为AD上的任一点,根据等高三角形的面积比等于对应底的比,即可求得
=
,
=
,继而求得答案;
拓展应用:由
=
=
,同理可得
=
,
=
,继而求得答案.
| 1 |
| 3 |
| S△ABE |
| S△ABD |
| 1 |
| 3 |
| S△ACE |
| S△ACD |
| 1 |
| 3 |
尝试探究:由AF⊥BC,EG⊥BC,易证得△EDG∽△ADB,然后由相似三角形的性质,求得
| EG |
| AF |
| S△BCE |
| S△ABC |
| S四边形ABEC |
| S△ABC |
类比延伸:由E为AD上的任一点,根据等高三角形的面积比等于对应底的比,即可求得
| S△ABE |
| S△ABD |
| AE |
| AD |
| S△ACE |
| S△ACD |
| AE |
| AD |
拓展应用:由
| S△ABE+S△ACE |
| S△ABD+S△ACD |
| S△ABE+S△ACE |
| S△ABC |
| AE |
| AD |
| S△BCE+S△ABE |
| S△ABC |
| BE |
| BF |
| S△ACE+S△BCE |
| S△ABC |
| CE |
| CG |
解答:解:问题引入:∵在△ABC中,D是BC上一点,AE=
AD,
∴
=
,
=
,
∴
=
=
;
尝试探究:∵AE=
AD,
∴
=
,
∵AF⊥BC,EG⊥BC,
∴AF∥EG,
∴△EDG∽△ADB,
∴
=
=
;
∵
=
=
=
,
∴
=1-
=
;
故答案为:
,
,
;
类比延伸:
=
,
∵E为AD上的一点,
∴
=
,
=
,
∴
=
=
;
拓展应用:∵
=
=
,
同理:
=
,
=
,
∴
+
+
=
=2.
| 1 |
| 3 |
∴
| S△ABE |
| S△ABD |
| 1 |
| 3 |
| S△ACE |
| S△ACD |
| 1 |
| 3 |
∴
| S四边形ABEC |
| S△ABC |
| S△ABE+S△ACE |
| S△ABD+S△ACD |
| 1 |
| 3 |
尝试探究:∵AE=
| 1 |
| 3 |
∴
| ED |
| AD |
| 2 |
| 3 |
∵AF⊥BC,EG⊥BC,
∴AF∥EG,
∴△EDG∽△ADB,
∴
| EG |
| AF |
| DE |
| AD |
| 2 |
| 3 |
∵
| S△BCE |
| S△ABC |
| ||
|
| EG |
| AF |
| 2 |
| 3 |
∴
| S四边形ABEC |
| S△ABC |
| 2 |
| 3 |
| 1 |
| 3 |
故答案为:
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
类比延伸:
| S四边形ABEC |
| S△ABC |
| AE |
| AD |
∵E为AD上的一点,
∴
| S△ABE |
| S△ABD |
| AE |
| AD |
| S△ACE |
| S△ACD |
| AE |
| AD |
∴
| S四边形ABEC |
| S△ABC |
| S△ABE+S△ACE |
| S△ABD+S△ACD |
| AE |
| AD |
拓展应用:∵
| S△ABE+S△ACE |
| S△ABD+S△ACD |
| S△ABE+S△ACE |
| S△ABC |
| AE |
| AD |
同理:
| S△BCE+S△ABE |
| S△ABC |
| BE |
| BF |
| S△ACE+S△BCE |
| S△ABC |
| CE |
| CG |
∴
| AE |
| AD |
| BE |
| BF |
| CE |
| CG |
| 2(S△ABE+S△BCE+S△ACE) |
| S△ABC |
点评:此题考查了面积与等积变换的知识.此题难度较大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列分式中是最简分式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 将一副三角板如图叠放,AB∥CD,则
将一副三角板如图叠放,AB∥CD,则| AO |
| OC |
| A、1:2 | ||
| B、2:3 | ||
C、1:
| ||
D、
|
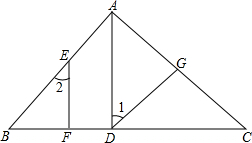 如图,在△ABC中,AD⊥BC于点D,EF⊥BC于点F,∠B=∠GDC,试说明∠1=∠2的理由.
如图,在△ABC中,AD⊥BC于点D,EF⊥BC于点F,∠B=∠GDC,试说明∠1=∠2的理由.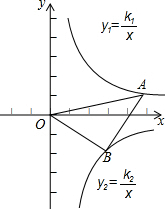 如图,在平面直角坐标系中,反比例函数y1=
如图,在平面直角坐标系中,反比例函数y1=