题目内容
如图,直线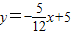 与x轴、y轴的交点分别为A、B,点M在线段AB上,且AM=6,动点P从点O出发以每秒2个单位长度的速度沿x轴向点A运动(点P与点O、A 均不重合).设点P运动t秒时,△APM的面积为S.
与x轴、y轴的交点分别为A、B,点M在线段AB上,且AM=6,动点P从点O出发以每秒2个单位长度的速度沿x轴向点A运动(点P与点O、A 均不重合).设点P运动t秒时,△APM的面积为S.(1)求S与t之间的函数关系式(写出自变量的取值范围);
(2)在运动过程中,是否存在S=
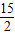 的情形?若存在,请判断此时△APM的形状,并说明理由;若不存在,请说明理由;
的情形?若存在,请判断此时△APM的形状,并说明理由;若不存在,请说明理由;(3)在运动过程中,当△APM为等腰三角形时,求t的值.
【答案】分析:(1)过M作MD⊥OA于D,先通过一次函数的解析式求得A与B的坐标,得到OA,OB和AB的长;易证得Rt△AMD∽Rt△ABO,通过相似比可求出MD=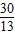 ,AD=
,AD= ,而PA=12-2t,再根据三角形的面积公式得到S与t之间的函数关系式;
,而PA=12-2t,再根据三角形的面积公式得到S与t之间的函数关系式;
(2)由S=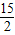 和(1)的函数关系得到-
和(1)的函数关系得到-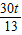 +
+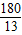 =
=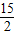 ,解方程得到t的值,得到PA的长,根据三角形相似的判定得到△APM∽△ABO,则∠AMP=∠AOB=90°;
,解方程得到t的值,得到PA的长,根据三角形相似的判定得到△APM∽△ABO,则∠AMP=∠AOB=90°;
(3)分类讨论:利用等腰三角形的性质得到线段相等,建立关于t的方程.当MP=MA,则AP=2AD,12-2t=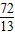 ×2;当AM=AP,则12-2t=6;当PA=PM,过P作PC⊥MA于C,
×2;当AM=AP,则12-2t=6;当PA=PM,过P作PC⊥MA于C,
易得Rt△APC∽Rt△ABO,则PA:AB=AC:AO,得到PA=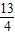 ,则12-2t=
,则12-2t=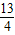 ,分别解方程即可.
,分别解方程即可.
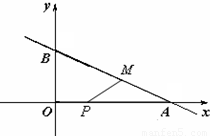
解答:解:(1)过M作MD⊥OA于D,如图,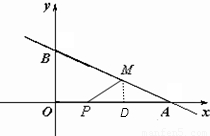
令x=0,y=5;令y=0,x=12,
∴OA=12,OB=5,
∴AB=13,
∵MD∥OB,
∴Rt△AMD∽Rt△ABO,
∴MD:OB=AD:AO=AM:AB,
而AM=6,
∴MD=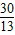 ,AD=
,AD=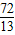 ,
,
又OP=2t,则PA=12-2t,
∴S= MD•PA=
MD•PA= •
•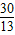 •(12-2t)=-
•(12-2t)=-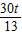 +
+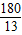 (0<t<6);
(0<t<6);
(2)存在S=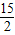 的情形,此时△APM为直角三角形.理由如下:
的情形,此时△APM为直角三角形.理由如下:
∵-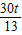 +
+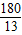 =
=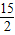 ,
,
∴t=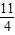 ,
,
∴PA=12-2t=12-2×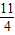 =
=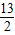 ,
,
∴AP:AB=AM:AO=1:2,
而∠PAM=∠BAO,
∴△APM∽△ABO,
∴∠AMP=∠AOB=90°,
即△APM是以AP为斜边的直角三角形;
(3)当MP=MA,
∴DP=DA,即AP=2AD,
∴12-2t=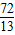 ×2,
×2,
∴t=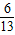 ;
;
当AM=AP,
∴12-2t=6,
∴t=3;
当PA=PM,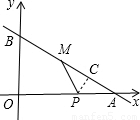 过P作PC⊥MA于C,如右图,
过P作PC⊥MA于C,如右图,
∴AC=MC=3,
∵Rt△APC∽Rt△ABO,
∴PA:AB=AC:AO,即PA:13=3:12,
∴PA=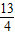 ,
,
∴12-2t=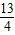 ,
,
∴t=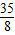 ;
;
所以△APM为等腰三角形时,t的值为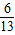 秒或3秒或
秒或3秒或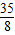 秒.
秒.
点评:本题考查了一次函数与三角形相似的综合运用:利用一次函数确定线段的长度,根据三角形相似的判定与性质建立函数关系和方程.也考查了等腰三角形的性质以及分类讨论思想的运用.
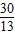 ,AD=
,AD= ,而PA=12-2t,再根据三角形的面积公式得到S与t之间的函数关系式;
,而PA=12-2t,再根据三角形的面积公式得到S与t之间的函数关系式;(2)由S=
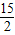 和(1)的函数关系得到-
和(1)的函数关系得到-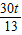 +
+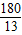 =
=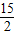 ,解方程得到t的值,得到PA的长,根据三角形相似的判定得到△APM∽△ABO,则∠AMP=∠AOB=90°;
,解方程得到t的值,得到PA的长,根据三角形相似的判定得到△APM∽△ABO,则∠AMP=∠AOB=90°;(3)分类讨论:利用等腰三角形的性质得到线段相等,建立关于t的方程.当MP=MA,则AP=2AD,12-2t=
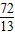 ×2;当AM=AP,则12-2t=6;当PA=PM,过P作PC⊥MA于C,
×2;当AM=AP,则12-2t=6;当PA=PM,过P作PC⊥MA于C,易得Rt△APC∽Rt△ABO,则PA:AB=AC:AO,得到PA=
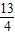 ,则12-2t=
,则12-2t=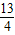 ,分别解方程即可.
,分别解方程即可.解答:解:(1)过M作MD⊥OA于D,如图,

令x=0,y=5;令y=0,x=12,
∴OA=12,OB=5,
∴AB=13,
∵MD∥OB,
∴Rt△AMD∽Rt△ABO,
∴MD:OB=AD:AO=AM:AB,
而AM=6,
∴MD=
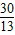 ,AD=
,AD=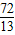 ,
,又OP=2t,则PA=12-2t,
∴S=
 MD•PA=
MD•PA= •
•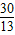 •(12-2t)=-
•(12-2t)=-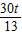 +
+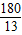 (0<t<6);
(0<t<6);(2)存在S=
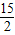 的情形,此时△APM为直角三角形.理由如下:
的情形,此时△APM为直角三角形.理由如下:∵-
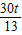 +
+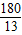 =
=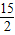 ,
,∴t=
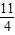 ,
,∴PA=12-2t=12-2×
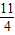 =
=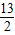 ,
,∴AP:AB=AM:AO=1:2,
而∠PAM=∠BAO,
∴△APM∽△ABO,
∴∠AMP=∠AOB=90°,
即△APM是以AP为斜边的直角三角形;
(3)当MP=MA,
∴DP=DA,即AP=2AD,
∴12-2t=
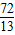 ×2,
×2,∴t=
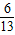 ;
;当AM=AP,
∴12-2t=6,
∴t=3;
当PA=PM,
 过P作PC⊥MA于C,如右图,
过P作PC⊥MA于C,如右图,∴AC=MC=3,
∵Rt△APC∽Rt△ABO,
∴PA:AB=AC:AO,即PA:13=3:12,
∴PA=
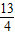 ,
,∴12-2t=
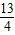 ,
,∴t=
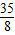 ;
;所以△APM为等腰三角形时,t的值为
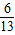 秒或3秒或
秒或3秒或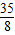 秒.
秒.点评:本题考查了一次函数与三角形相似的综合运用:利用一次函数确定线段的长度,根据三角形相似的判定与性质建立函数关系和方程.也考查了等腰三角形的性质以及分类讨论思想的运用.

练习册系列答案
相关题目
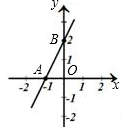 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.
 3、如图,直线与y轴的交点是(0,-3),则当x<0时,( )
3、如图,直线与y轴的交点是(0,-3),则当x<0时,( ) 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点. 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.