题目内容
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。

(1)尝试探究
在图1中,过点E作 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是
,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是
,  的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若 则
则 的值是
(用含
的值是
(用含 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。

(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若 ,则
,则 的值是
(用含
的值是
(用含 的代数式表示).
的代数式表示).

【答案】
(1)
(2)
(3)
【解析】
(1)∵ ,
,
∴
∵E为BC中点, ,∴H为BG中点,
,∴H为BG中点,
∴CG=2EH
四边形ABCD为菱形,AB=BC=CD=DA=3EH
∴
(2)作EH∥AB交BG于点H,则
∴
∵AB=CD,∴
EH∥AB∥CD,∴
∴ ,∴CG=2EH
,∴CG=2EH
∴
(3)过E作EH∥AB,交BD延长线于点H
由题意可知:EH∥DC∥AB
∴

又∵
化简得:

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目


 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。
 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 则
则 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。
 ,则
,则 的值是 (用含
的值是 (用含 的代数式表示).
的代数式表示).
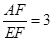 ,求
,求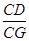 的值。
的值。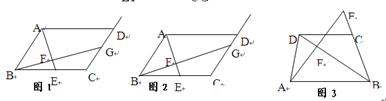
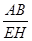 的值是 ,
的值是 ,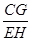 的值是
的值是 ,则
,则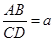 ,
,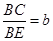 (a>0,b>0),则
(a>0,b>0),则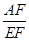 的值是 。(用含a、b的代数式表示)写出解答过程。
的值是 。(用含a、b的代数式表示)写出解答过程。 ,求
,求 的值。
的值。
 的值是 ,
的值是 , 的值是
的值是 ,则
,则 ,
, (a>0,b>0),则
(a>0,b>0),则 的值是 。(用含a、b的代数式表示)写出解答过程。
的值是 。(用含a、b的代数式表示)写出解答过程。