题目内容
如图,在平面直角坐标系中,抛物线 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)判断∆ABC的形状,并说明理由;
(2)如图1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交x轴于点E.当∆PBC面积的最大值时,点F为线段BC一点(不与点、重合),连接EF,动点G从点E出发,沿线段EF以每秒1个单位的速度运动到点F,再沿FC以每秒 个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
(3)如图2,将∆ACO沿射线CB方向以每秒 个单位的速度平移,记平移后的∆ACO为∆A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当∆A MC1为等腰三角形时,求t的值.
个单位的速度平移,记平移后的∆ACO为∆A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当∆A MC1为等腰三角形时,求t的值.


练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
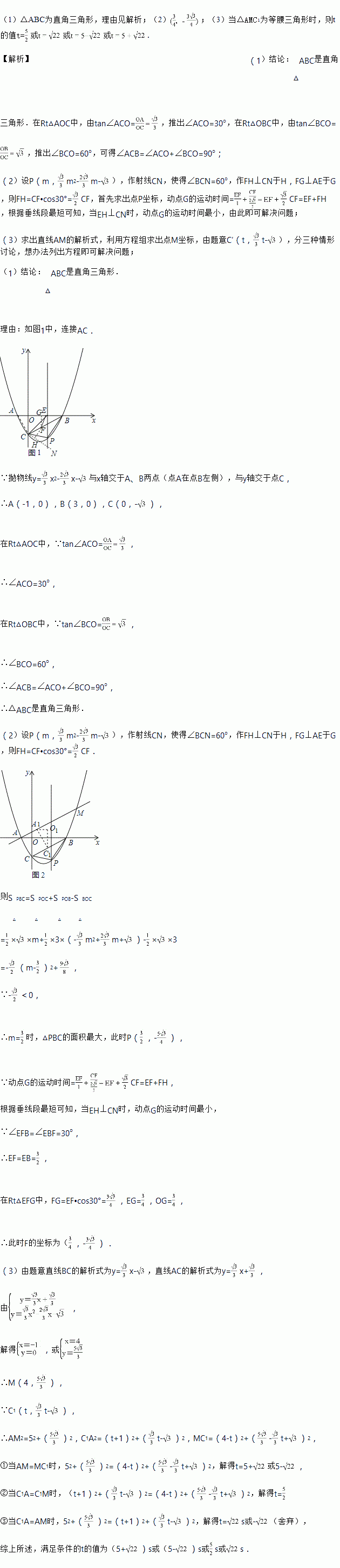

 ,
,  , -
, - , 0, -
, 0, - ,
,  ,-
,- ,
, , 3.14
, 3.14
 的值为0,则( )
的值为0,则( )






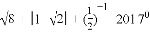 =____________.
=____________.




